题目内容
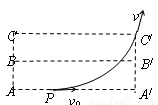
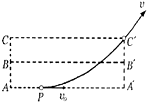 如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面,相邻等势面间的距离为0.5cm,其中B B'为零势能面.一个质量为m,带电量为+q的粒子沿AA′方向以初动能EK自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( )
如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面,相邻等势面间的距离为0.5cm,其中B B'为零势能面.一个质量为m,带电量为+q的粒子沿AA′方向以初动能EK自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( )分析:根据等势面的分布情况和粒子的轨迹分析可知:粒子做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动.粒子从A到C,水平位移为x=2cm,竖直位移为y=1cm,由x=v0t,y=
t,求出vy,由速度的合成求出v,再求出该粒子到达C′点时的动能.粒子运动中电势能和动能总量守恒,根据能量守恒定律确定粒子的总能量,再求出粒子经过P、C′点时的电势能.
| vy |
| 2 |
解答:解:AB、粒子做类平抛运动,水平方向做匀速直线运动,有x=v0t,竖直方向做匀加速直线运动有y=
t.
由题x=2cm,竖直位移为y=1cm,得到vy=v0,v=
v0,该粒子到达C′点时的动能是EK=
mv2=2?
mv02=2EK.
由于相邻等势面间的距离相等,电势差相等,动能的增量相等,则该粒子通过等势面BB'时的动能是1.5Ek.故A正确,B错误.
C、BB'为零势能面,由上可知,粒子经过等势面BB'时总能量为是1.5Ek,该粒子在P点时的电势能是1.5Ek-Ek=0.5Ek.故C错误.
D、根据能量守恒得,该粒子到达C′点时的电势能EP=1.5Ek-2EK=-0.5Ek.故D错误.
故选:A.
| vy |
| 2 |
由题x=2cm,竖直位移为y=1cm,得到vy=v0,v=
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于相邻等势面间的距离相等,电势差相等,动能的增量相等,则该粒子通过等势面BB'时的动能是1.5Ek.故A正确,B错误.
C、BB'为零势能面,由上可知,粒子经过等势面BB'时总能量为是1.5Ek,该粒子在P点时的电势能是1.5Ek-Ek=0.5Ek.故C错误.
D、根据能量守恒得,该粒子到达C′点时的电势能EP=1.5Ek-2EK=-0.5Ek.故D错误.
故选:A.
点评:本题首先要分析出粒子做类平抛运动,其次技巧是研究粒子经过BB'面时总能量,根据能量守恒研究经过其他等势面时的电势能.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
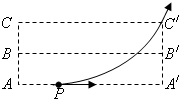 如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初动能Ek自图中的P点进入电场.刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( )
如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初动能Ek自图中的P点进入电场.刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( )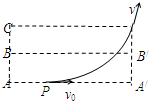 (2011?徐州模拟)如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面,相邻等势面间的距离均为0.5cm,其中BB'为零势能面.一个质量为m,带电量为+q的粒子沿AA′方向以初动能Ek自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( )
(2011?徐州模拟)如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面,相邻等势面间的距离均为0.5cm,其中BB'为零势能面.一个质量为m,带电量为+q的粒子沿AA′方向以初动能Ek自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm.粒子的重力忽略不计.下列说法中正确的是( ) ′、
′、 ′、
′、 ′是该电场的三个等势面,相邻等势面间的距离均为0.5 cm,其中
′是该电场的三个等势面,相邻等势面间的距离均为0.5 cm,其中 ,带电量为+
,带电量为+ 的粒子沿从
的粒子沿从 自图中的
自图中的 点进入电场,刚好从
点进入电场,刚好从 ′点离开电场。已知
′点离开电场。已知 ′=2 cm。粒子的重力忽略不计。下列说法中正确的是
′=2 cm。粒子的重力忽略不计。下列说法中正确的是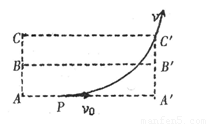
 、
、 、
、 是该电场的三个等势面,相邻等势面间的距离均为0.5cm,其中
是该电场的三个等势面,相邻等势面间的距离均为0.5cm,其中 点离开电场。已知
点离开电场。已知 =2cm。粒子的重力忽略不计。下列说法中正确的是 ( )
=2cm。粒子的重力忽略不计。下列说法中正确的是 ( )