题目内容
一个物体原来静止在光滑的水平地面上,从t=0开始运动,在第1、3、5、……奇数秒内,给物体施加方向向北的水平推力,使物体获得大小为2m/s2的加速度,在第2、4、6、……偶数秒内,撤去水平推力,向经过多长时间,物体位移的大小为40.25m?
方法一:物体在奇数秒内做匀加速直线运动,加速度大小为 ;在偶数秒内做匀速直线运动;直观地描述物体的运动可以借助速度---时间图象,如图2-5所示为该物体的运动的速度---时间图像,物体在第1S内的位移为1m,第2S内的位移为2m,第3S内的位移为3m,由此规律可得物体在整数秒内的位移S=
;在偶数秒内做匀速直线运动;直观地描述物体的运动可以借助速度---时间图象,如图2-5所示为该物体的运动的速度---时间图像,物体在第1S内的位移为1m,第2S内的位移为2m,第3S内的位移为3m,由此规律可得物体在整数秒内的位移S= ×n〈40.25得n<9,物体在8S内的位移为36m,余下的4.25m将在9S的部分时间内完成,8S末物体的速度为
×n〈40.25得n<9,物体在8S内的位移为36m,余下的4.25m将在9S的部分时间内完成,8S末物体的速度为 ,4.25=8t+
,4.25=8t+ ×
× 解得t=0.5S,所以物体总共用8.5S。方法二:物体在第1S、2S、……nS内的位移分别为S1、S2、……Sn,则有: S1=
解得t=0.5S,所以物体总共用8.5S。方法二:物体在第1S、2S、……nS内的位移分别为S1、S2、……Sn,则有: S1= a?1
a?1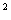 =1m S2=a?1?1=2m S3=a?1?1+
=1m S2=a?1?1=2m S3=a?1?1+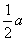 ?1
?1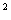 =3m …… Sn=n?m令 S1+S2+……+Sn=40.25即1+2+……+n=40.25
=3m …… Sn=n?m令 S1+S2+……+Sn=40.25即1+2+……+n=40.25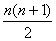 =40.25解得: 8<n<9,物体在前8S内的位移为1+2+……+8=
=40.25解得: 8<n<9,物体在前8S内的位移为1+2+……+8=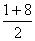 ×8=36m,物体在9S内的初速度为8S末的速度,其大小为8m/S.在9S内完成剩余的(40.25-36)=4.25的位移所用的时间为: 4.25=V8t+
×8=36m,物体在9S内的初速度为8S末的速度,其大小为8m/S.在9S内完成剩余的(40.25-36)=4.25的位移所用的时间为: 4.25=V8t+ 4.25=8t’+
4.25=8t’+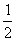 ×2×t’
×2×t’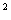 t’=0.5S所以物体完成40.25m的位移总共所用的时间为(8+0.5)=8.5S
t’=0.5S所以物体完成40.25m的位移总共所用的时间为(8+0.5)=8.5S

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目