题目内容
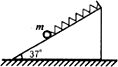如图所示，一轻质弹簧的一端系一质量为m的小球，另一端固定在倾角为37°的光滑斜面体顶端，弹簧与斜面平行．在斜面体以大小为g的加速度水平向左做匀加速直线运动的过程中，小球始终相对于斜面静止．已知弹簧的劲度系数为k，则该过程中弹簧的形变量为（已知：sin37°=0.6，cos37°=0.8）（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
分析：以小球为研究对象，根据牛顿第二定律和胡克定律列式，求解弹簧的形变量．
解答：解：将加速度分解为沿斜面和垂直于斜面方向．
以小球为研究对象，根据牛顿第二定律和胡克定律得：
沿斜面方向有：mgsin37°+kx=macos37°
又a=g
解得：x=
故选：A．
以小球为研究对象，根据牛顿第二定律和胡克定律得：
沿斜面方向有：mgsin37°+kx=macos37°
又a=g
解得：x=
| mg |
| 5k |
故选：A．
点评：本题关键要灵活运用正交分解法，将加速度分解比较简洁，也可以分解力，列出两个方程求解．
练习册系列答案
相关题目
如图所示，一轻质弹簧竖直放置，下端固定在水平面上，上端处于a位置．当一重球放在弹簧上端静止时，弹簧上端被压缩到b位置．现将重球（视为质点）轻放在弹簧a处，由静止释放后，球沿弹簧中轴线向下运动到最低点c处的过程中，下列说法正确的是（ ）
如图所示，一轻质弹簧与质量为m的物体组成弹簧振子，物体在同一条竖直线上的A、B间做简谐运动，O为平衡位置，C为AO的中点，已知OC=h，振子的周期为T．某时刻物体恰好经过C点并向上运动，则从此时刻开始的半个周期时间内，下列判断正确的是（ ）
如图所示，一轻质弹簧固定在水平地面上，O点为弹簧原长时上端的位置，一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上，物体压缩弹簧到最低点B 后向上运动．则以下说法正确的是（ ）