题目内容
【题目】如图所示，在xOy平面内，以O1(0，R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1，x轴下方有一直线ab，ab与x轴相距为d，x轴与直线ab间区域有平行于y轴的匀强电场E，在ab的下方有一平行于x轴的感光板MN，ab与MN间区域有垂直于纸平面向外的匀强磁场B2.在0≤y≤2R的区域内，质量为m的电子从圆形区域左侧的任何位置沿x轴正方向以速度v0射入圆形区域，经过磁场B1偏转后都经过O点，然后进入x轴下方．已知x轴与直线ab间匀强电场场强大小
，ab与MN间磁场磁感应强度
.不计电子重力．
(1)求圆形区域内磁场磁感应强度B1的大小？
(2)若要求从所有不同位置出发的电子都不能打在感光板MN上，MN与ab板间的最小距离h1是多大？
(3)若要求从所有不同位置出发的电子都能打在感光板MN上，MN与ab板间的最大距离h2是多大？当MN与ab板间的距离最大时，电子从O点到MN板，运动时间最长是多少？
【答案】(1) 
；(2)3d (3)d ； 
【解析】试题分析：（1）抓住所有电子射入圆形区域后做圆周运动轨道半径大小相等，根据几何关系得出粒子在磁场中的运动半径，结合半径公式求出圆形区域内磁场磁感应强度B1的大小．（2）根据动能定理求出粒子进入磁场下方磁场的速度，根据半径公式求出粒子的半径，根据几何关系求出粒子进入磁场时速度方向与水平方向的夹角，通过几何关系求出MN与ab板间的最小距离．（3）如果电子在O点沿x轴正方向射入电场，经电场偏转和磁场偏转后，能打在感光板上，则所有电子都能打在感光板上．根据几何关系求出MN与ab板间的最大距离．
作出粒子的运动轨迹，根据粒子在电场和磁场中的运动时间求出运动的最长时间．
（1）所有电子射入圆形区域后做圆周运动，轨道半径大小相等，设为r，当从位置y=R处射入的电子经过O点进入x轴下方，则： 
， 
，解得
（2）设电子经电场加速后到达ab时速度大小为v，电子在ab与MN间磁场做匀速圆周运动轨道半径为r1，沿x轴负方向射入电场的电子离开电场进入磁场时速度方向与水平方向成θ角，则
， 
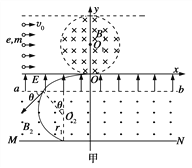
如果电子在O点以速度v0沿x轴负方向射入电场，经电场偏转和磁场偏转后，不能打在感光板上，则所有电子都不能打在感光板上．恰好不能打在感光板上的电子在磁场中的圆轨道圆心为O2，如图甲所示
则感光板与ab间的最小距离
解得
（3）如果电子在O点沿x轴正方向射入电场，经电场偏转和磁场偏转后，能打在感光板上，则所有电子都能打在感光板上．恰好能打在感光板上的电子在磁场中的圆轨道圆心为O3，如图乙所示．
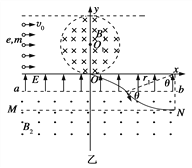
感光板与ab间的最大距离
，解得
当感光板与ab间的距离最大为
时，所有从O点到MN板的电子中，沿x轴正方向射入电场的电子，运动时间最长．设该电子在匀强电场中运动的加速度为a，运动时间为
，在磁场
中运动周期为T，时间为
，则
， 
运动最长时间
解得
， 
， 
， 
