题目内容
如图甲所示,一个电阻值为R,匝数为n的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路。线圈的半径为r1。在线圈中半径为r2的圆形区域内存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图乙所示,图线与横、纵轴的截距分别为t0和B0。导线的电阻不计,求0至t1时间内
(1)通过电阻R1上的电流大小及方向。
(2)通过电阻R1上的电荷量q。
(1) 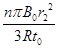 电流由b向a通过R1(2)
电流由b向a通过R1(2) 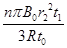
解析试题分析:(1)由法拉第电磁感应定律得感应电动势为
E=n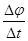 =
=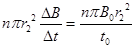
由闭合电路的欧姆定律,得通过R1的电流大小为
I=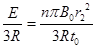
由楞次定律知该电流由b向a通过R1 6分
(2)由I=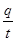 得在0至t1时间内通过R1的电量为
得在0至t1时间内通过R1的电量为
q=It1=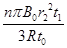 6分
6分
考点:考查法拉第电磁感应定律
点评:本题难度较小,应用法拉第电磁感应定律求解问题时,应首先明确产生感应电流的原因,选择合适的公式求解

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
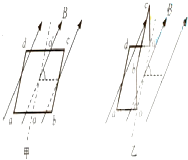 如图甲所示,一个电阻为R面积为S的矩形导线框abcd,水平放置在匀强磁场中,磁场的磁感应强度为B,方向与ad边垂直并与线框平面成30°角,o.o′分别是ab和cd边的中点.现将线框右半边obco‘绕oo′逆时针旋转90°到图乙所示位置.在这一过程中,导线中通过的电荷量是 ( )
如图甲所示,一个电阻为R面积为S的矩形导线框abcd,水平放置在匀强磁场中,磁场的磁感应强度为B,方向与ad边垂直并与线框平面成30°角,o.o′分别是ab和cd边的中点.现将线框右半边obco‘绕oo′逆时针旋转90°到图乙所示位置.在这一过程中,导线中通过的电荷量是 ( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
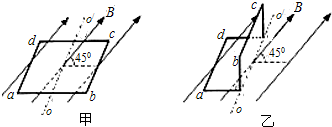 (2009?安徽)如图甲所示,一个电阻为R,面积为S的矩形导线框abcd,水平旋转在匀强磁场中,磁场的磁感应强度为B,方向与ad边垂直并与线框平面成45°角,o、o′分别是ab和cd边的中点.现将线框右半边obco′绕oo′逆时针90°到图乙所示位置.在这一过程中,导线中通过的电荷量是( )
(2009?安徽)如图甲所示,一个电阻为R,面积为S的矩形导线框abcd,水平旋转在匀强磁场中,磁场的磁感应强度为B,方向与ad边垂直并与线框平面成45°角,o、o′分别是ab和cd边的中点.现将线框右半边obco′绕oo′逆时针90°到图乙所示位置.在这一过程中,导线中通过的电荷量是( )

 B.
B. C.
C. D.0
D.0

 B.
B.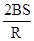 C.
C. D.0
D.0