Question

（ 24分）物理小组的同学在寒冷的冬天做了一个这样的实验：他们把一个实心的大铝球加热到某温度，然后把它放在结冰的湖面上（冰层足够厚），铝球便逐渐陷入冰内．当铝球不再下陷时，测出球的最低点陷入冰中的深度．将铝球加热到不同的温度，重复上述实验8次，最终得到如下数据：

实验顺序数	1	2	3	4	5	6	7	8
热铝球的温度 t /℃	55	70	85	92	104	110	120	140
陷入深度 h /cm	9.0	12.9	14.8	16.0	17.0	18.0	17.0	16.8

已知铝的密度约为水的密度的3倍，设实验时的环境温度及湖面冰的温度均为 0℃．已知此情况下，冰的熔解热．

1．试采用以上某些数据估算铝的比热．

2．对未被你采用的实验数据，试说明不采用的原因，并作出解释．

Answer 1

六、参考解答

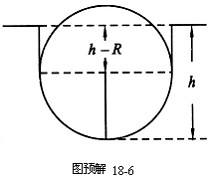
铝球放热，使冰熔化．设当铝球的温度为时，能熔化冰的最大体积恰与半个铝球的体积相等，即铝球的最低点下陷的深度与球的半径相等．当热铝球的温度时，铝球最低点下陷的深度，熔化的冰的体积等于一个圆柱体的体积与半个铝球的体积之和，如图预解18-6-1所示．

设铝的密度为，比热为，冰的密度为，熔解热为，则铝球的温度从℃降到0℃的过程中，放出的热量

                           （1）

熔化的冰吸收的热量

                                    （2）

假设不计铝球使冰熔化过程中向外界散失的热量，则有

                                                            （3）

解得

                                                     （4）

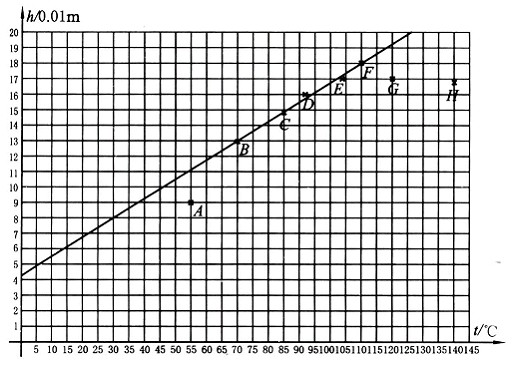
即与成线形关系．此式只对时成立。将表中数据画在图中，得第1，2，…，8次实验对应的点、、…、。数据点、、、、五点可拟合成一直线，如图预解18-6-2所示。此直线应与（4）式一致．这样，在此直线上任取两点的数据，代人（4）式，再解联立方程，即可求出比热的值．例如，在直线上取相距较远的横坐标为8和100的两点和，它们的坐标由图预解18-6-2可读得为

                    

将此数据及的值代入（4）式，消去，得

                                                 （5）

2. 在本题作的图预解18-6-2中，第1，7，8次实验的数据对应的点偏离直线较远，未被采用．这三个实验数据在图上的点即、、．

点为什么偏离直线较远？因为当时，从（4）式得对应的温度℃，（4）式在的条件才成立。但第一次实验时铝球的温度℃＜，熔解的冰的体积小于半个球的体积，故（4）式不成立．

、为什么偏离直线较远？因为铝球的温度过高（120℃、140℃），使得一部分冰升华成蒸气，且因铝球与环境的温度相差较大而损失的热量较多，（2）、（3）式不成立，因而（4）式不成立．

评分标准：本题24分

第1问17分；第二问7分。第一问中，（1）、（2）式各3分；（4）式4分。正确画出图线4分；解出（5）式再得3分。第二问中，说明、、点不采用的原因给1分；对和、偏离直线的原因解释正确，各得3分。