题目内容
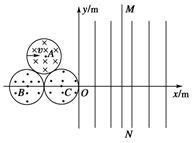
在坐标系xOy中,有三个靠在一起的等大的圆形区域,分别存在着方向如图所示的匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径r=![]() m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形区域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求:
m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形区域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求:
(1)该离子通过磁场区域所用的时间.
(2)离子离开磁场区域的出射点偏离最初入射方向的侧移为多大?(侧移指垂直初速度方向上移动的距离)
(3)若在匀强电场区域内竖直放置一挡板MN,欲使离子打到挡板MN上的偏离最初入射方向的侧移为零,则挡板MN应放在何处?匀强电场的方向如何?
(1)(6分)4.19×10-6s (2)(5分)2m
(3)(7分)MN应放在距y轴2![]() m的位置上 竖直向下
m的位置上 竖直向下
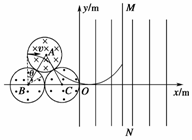
[解析] (1)离子在磁场中做匀速圆周运动,在A、C两区域的运动轨迹是对称的,如图所示,设离子做圆周运动的半径为R,圆周运动的周期为T,由牛顿第二定律得:qvB=m![]()
又T=![]()
解得:R=![]() ,T=
,T=![]()
将已知量代入得:R=2m …………2分
设θ为离子在区域A中的运动轨迹所对应圆心角的一半,由几何关系可知离子在区域A中运动轨迹的圆心恰好在B点,
则:tanθ=![]() =
=![]()
θ=30° …………2分
则离子通过磁场区域所用的时间为:
t=![]() =4.19×10-6s ……2分
=4.19×10-6s ……2分
(2)由对称性可知:离了从原点O处水平射出磁场区域,由图可知侧移为
d=2rsin2θ=2m …………5分
(3)欲使离子打到挡板MN上时偏离最初入射方向的侧移为零,则离子在电场中运动时受到的电场力方向应向上,所以匀强电场的方向向下
离子在电场中做类平抛运动,加速度大小为:
a=Eq/m=5.0×1011m/s2 …………2分
沿y方向的位移为:
y=![]() at2=d …………2分
at2=d …………2分
沿x方向的位移为:x=vt …………2分
解得:x=2![]() m …………1分
m …………1分
所以MN应放在距y轴2![]() m的位置.
m的位置.

 如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,下边界与x轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是如图中的( )
如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,下边界与x轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是如图中的( ) (2011?河南模拟)如图所示,在坐标系xOy中,有边长为a的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i随时间t变化的图线是( )
(2011?河南模拟)如图所示,在坐标系xOy中,有边长为a的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i随时间t变化的图线是( )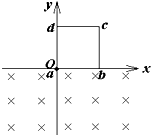 如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条边ab和x轴重合、顶点a位于坐标原点O处.在x轴的下方有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合.t=0时刻,线圈以恒定的角速度ω绕过a点垂直于坐标平面的轴顺时针转动,穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i随时间t变化的图线是图中的( )
如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条边ab和x轴重合、顶点a位于坐标原点O处.在x轴的下方有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合.t=0时刻,线圈以恒定的角速度ω绕过a点垂直于坐标平面的轴顺时针转动,穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i随时间t变化的图线是图中的( )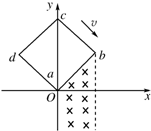 (2011?浙江模拟)如图所示,在坐标系xOy中,有边长为a的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )
(2011?浙江模拟)如图所示,在坐标系xOy中,有边长为a的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( ) (2013?怀化二模)如图所示,在坐标系xOy中,有边长为a的正方形均匀铜线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行,下边界足够远.t=0时刻,线圈以恒定的速度V(平动)沿垂直于磁场上边界的方向穿过磁场区域.则在线圈穿越磁场区域的过程中,ab间的电势差Uab随时间t变化的图线是下图中的( )
(2013?怀化二模)如图所示,在坐标系xOy中,有边长为a的正方形均匀铜线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行,下边界足够远.t=0时刻,线圈以恒定的速度V(平动)沿垂直于磁场上边界的方向穿过磁场区域.则在线圈穿越磁场区域的过程中,ab间的电势差Uab随时间t变化的图线是下图中的( )