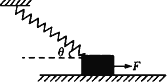
��Ŀ����
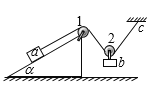
����Ŀ��һ��������n��![]() �����β���ש�ĺ������ͼ��ʾ�������Կ����������������OABΪֱ������������B��30����OACΪ������OΪԲ������AOC��90����B����ǽ�ڽӴ�����MN�ABC��һ����ɫ�⾭������AC����O�㣬�������30���������ǽ��MN�ϳ���������ߣ���֪OB����ΪL����
�����β���ש�ĺ������ͼ��ʾ�������Կ����������������OABΪֱ������������B��30����OACΪ������OΪԲ������AOC��90����B����ǽ�ڽӴ�����MN�ABC��һ����ɫ�⾭������AC����O�㣬�������30���������ǽ��MN�ϳ���������ߣ���֪OB����ΪL����
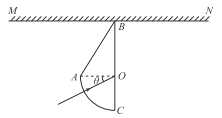
��i���������ľ��룻
��ii����������������������������������ٶ��ʱO�㲻����������������
���𰸡���i����![]() ��l��L��ii��45��
��l��L��ii��45��
���������⣺��i�������䵽ʱO���һ���ֹⷴ�䣬�ɹ�ķ��䶨�ɵ÷����Ϊ30�㡣�����������AB��ֱ������ֱ���䵽ǽ����E�㣬��ͼ��ʾ
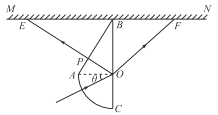
�ɼ��ι�ϵ��BE��![]() L
L
һ���ֹ����䣬�ɹ�����䶨����![]()
���i��45��
�ɼ��ι�ϵ�á�OBFΪ����ֱ�������Σ�BF��L
�������ľ���ΪBE��BF����![]() ��l��L
��l��L
��ii�����������O�������Ǵ��ڻ�����ٽ��ʱ��O�㲻����������������
����sinC��![]()
�������ݽ��C��45��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ