题目内容
14.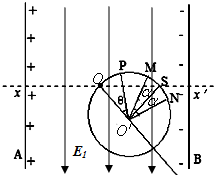 在光滑绝缘的水平面上,竖直放置两块无限长的平行金属板A、B,相距d=1.0m,两板间电压为U=2500V,同时两板间还存在电场强度为E1=2500N/C,方向水平且平行于金属板的匀强电场(忽略场的边缘效应),如图所示为俯视图.xox’为水平面上垂直两金属板的直线,O点与两板距离相等,在O点有一微粒源(忽略微粒源对微粒运动的影响),释放方向沿水平面质量m=2.5×10-3kg、带正电荷q=+1.0×10-5C的球形微粒(可看作点电荷).过O点作半径R=0.25m的圆,圆心O′在过O点右下方45°的直线上.P、M、S、N分布在圆周上,O′S与OO′垂直,∠OO′P=θ,∠MO′S=∠SO′N=α=30°. 不计电荷间的相互作用,求:
在光滑绝缘的水平面上,竖直放置两块无限长的平行金属板A、B,相距d=1.0m,两板间电压为U=2500V,同时两板间还存在电场强度为E1=2500N/C,方向水平且平行于金属板的匀强电场(忽略场的边缘效应),如图所示为俯视图.xox’为水平面上垂直两金属板的直线,O点与两板距离相等,在O点有一微粒源(忽略微粒源对微粒运动的影响),释放方向沿水平面质量m=2.5×10-3kg、带正电荷q=+1.0×10-5C的球形微粒(可看作点电荷).过O点作半径R=0.25m的圆,圆心O′在过O点右下方45°的直线上.P、M、S、N分布在圆周上,O′S与OO′垂直,∠OO′P=θ,∠MO′S=∠SO′N=α=30°. 不计电荷间的相互作用,求:(1)初速度为零的微粒运动到平行板的动能
(2)初速度大小不等,方向均与xox’成45°角斜向右上方,经过一段时间通过P点的微粒初速度v0与θ的关系
(3)确定在穿过圆周MSN段的微粒中,穿越时的最大动能和最小动能.
分析 (1)静止的带电微粒在重力与电场力作用下,使其动能增加,则由动能定理可求出微粒从O点到平行板的动能;
(2)微粒从O点开始作类平抛运动,因此可将此运动沿初速度方向与加速度方向进行分解,根据运动学规律可列式,从而求出通过P点的微粒初速度υ0与θ的关系;
(3)根据动能的表达中的θ来确定动能的最大值与最小值.
解答 解: (1)带电微粒在电场中受重力和电场力FE=qE=2.5×10-2N
(1)带电微粒在电场中受重力和电场力FE=qE=2.5×10-2N
G=mg=2.5×10-2N
则F合=$\sqrt{{F}_{E}^{2}+{G}^{2}}$=2.5$\sqrt{2}$×10-2N
因为FE=G,所以合力方向与水平方向成45°角斜右向下,
如图所示.
W合=△Ek
Ek=$\sqrt{2}$F合×$\frac{d}{2}$=2.5×10-2J
(2)
微粒做类平抛运动,则有:Rsinθ=v0t
且R-Rcosθ=$\frac{1}{2}a{t}^{2}$
根据牛顿第二定律,则有:F=ma
解得:v0=$\sqrt{\frac{5\sqrt{2}(1+cosθ)}{4}}$
(3)由上式结论得粒子从O点出发时的动能为Eko=$\frac{1}{2}$mυ02=$\frac{25\sqrt{2}×1{0}^{-3}(1+cosθ)}{16}$
从O到P过程中,由动能定理,$\sqrt{2}qER(1-cosθ)=\frac{1}{2}m{v}_{P}^{2}-\frac{1}{2}m{v}_{0}^{2}$
则经过P点时的动能为:EKP=$\frac{1}{2}$mυ02+$\sqrt{2}$qE(R-Rcosθ)=$\frac{25\sqrt{2}×1{0}^{-3}(5-3cosθ)}{16}$
可以看出,当θ从0°变化到180°,微粒穿越圆周时的动能逐渐增大,因此穿过M点的微粒动能最小,穿过N点的微粒动能最大.
最小动能为:EKM=$\frac{\sqrt{2}}{16}$mg(5-3cos60°)≈7.7×10-3 J
最大动能为:EKN=$\frac{\sqrt{2}}{16}$mg(5-3cos120°)≈0.0144J
答:(1)初速度为零的微粒运动到平行板的动能2.5×10-2J;
(2)经过一段时间通过P点的微粒初速度v0与θ的关系为$\sqrt{\frac{5\sqrt{2}(1+cosθ)}{4}}$;
(3)穿越时的最大动能7.7×10-3J和最小动能1.44×102J.
点评 考查动能定理、牛顿第二定律与运动学规律,涉及到直线运动中的匀加速与匀减速;曲线运动中的类平抛运动,同时体现处理平抛运动的规律.并由数学知识来确定动能的极大值与极小值.

| A. | 只有静止的物体才受到重力作用 | |
| B. | 一个挂在绳子上的物体,它受到的重力就是绳对它的拉力 | |
| C. | 重力没有施力物体 | |
| D. | 在地面上同一点,质量大的物体受到的重力大 |
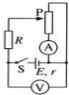
| A. | 电压表V读数先变大后变小,电流表A读数变大 | |
| B. | 电压表V读数先变小后变大,电流表A读数变小 | |
| C. | 电压表V读数先变大后变小,电流表A读数先变小后变大 | |
| D. | 电压表V读数先变小后变大,电流表A读数先变大后变小 |
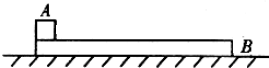
 如图所示,两平行金属板竖直放置,质量相等的两带电液滴1、2从左极板边缘的O点分别以一定初速度竖直向上射出,两液滴分别垂直击中右极板上的A、B两点,已知C点是右极板的下端点且AB=BC,则( )
如图所示,两平行金属板竖直放置,质量相等的两带电液滴1、2从左极板边缘的O点分别以一定初速度竖直向上射出,两液滴分别垂直击中右极板上的A、B两点,已知C点是右极板的下端点且AB=BC,则( )| A. | 液滴1、2的电荷量之比为1:2 | B. | 液滴1、2的电荷量之比为1:$\sqrt{2}$ | ||
| C. | 液滴1、2的初速度之比为2:1 | D. | 液滴1、2的初速度之比为1:$\sqrt{2}$ |
 如图为哈勃望远镜拍摄的银河系中被科学家称为“罗盘座T星”系统的照片,该系统是由一颗白矮星和它的类日伴星组成的双星系统,图片下面的亮点为白矮星,上面的部分为类日伴星(中央的最亮的为类似太阳的天体).由于白矮星不停地吸收由类日伴星抛出的物质致使其质量不断增加,科学家预计这颗白矮星在不到1000万年的时间内会完全“爆炸”,从而变成一颗超新星.现假设类日伴星所释放的物质被白矮星全部吸收,并且两星之间的距离在一段时间内不变,两星球的总质量不变,不考虑其它星球对该“罗盘座T星”系统的作用,则下列说法正确的是( )
如图为哈勃望远镜拍摄的银河系中被科学家称为“罗盘座T星”系统的照片,该系统是由一颗白矮星和它的类日伴星组成的双星系统,图片下面的亮点为白矮星,上面的部分为类日伴星(中央的最亮的为类似太阳的天体).由于白矮星不停地吸收由类日伴星抛出的物质致使其质量不断增加,科学家预计这颗白矮星在不到1000万年的时间内会完全“爆炸”,从而变成一颗超新星.现假设类日伴星所释放的物质被白矮星全部吸收,并且两星之间的距离在一段时间内不变,两星球的总质量不变,不考虑其它星球对该“罗盘座T星”系统的作用,则下列说法正确的是( )| A. | 两星之间的万有引力不变 | B. | 两星的运动周期不变 | ||
| C. | 类日伴星的轨道半径减小 | D. | 白矮星的线速度变小 |
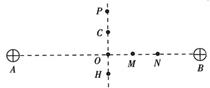 如图所示,两个点电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,M、N为AB连线上的两点,已知PC=CO=OH,OM=MN,取无穷远处电势为零,下列结论中正确的是( )
如图所示,两个点电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,M、N为AB连线上的两点,已知PC=CO=OH,OM=MN,取无穷远处电势为零,下列结论中正确的是( )| A. | C点和H点的电场强度相同 | |
| B. | OC与CP间的电势差相同 | |
| C. | MN两点间的电势差大于MO两点间的电势差 | |
| D. | 正检验电荷自C点由静止释放后将做加速度减小的变加速直线运动 |
| A. | 用手把一个重物压在竖直墙壁上,重物保持静止状态.当手对重物的压力变大时,重物所受摩擦力不变 | |
| B. | 静摩擦力的方向与运动的方向可以相同,也可以与运动的方向成任意夹角 | |
| C. | 物体受静摩擦力时可以静止,但物体受滑动摩擦力时一定不能处于静止状态 | |
| D. | 静摩擦力可以作为动力,但滑动摩擦力只能作为阻力 |
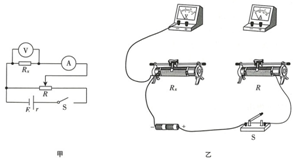 为检测一个标值为5Ω的滑动变阻器,现可供使用的器材如下:
为检测一个标值为5Ω的滑动变阻器,现可供使用的器材如下: