题目内容
7. 有一木块静止在光滑水平面上,木块质量=0.5kg,长L=1m,一个质量为m=1kg的小滑块,其尺寸远小于L,它与木板之间的动摩擦因数μ=0.2,g=10m/s2,某时刻滑块m一水平向右的初速度v0=4m/s,从左端滑上木板的上表面,同时对木板施加一个水平向右的恒定拉力F.求:
有一木块静止在光滑水平面上,木块质量=0.5kg,长L=1m,一个质量为m=1kg的小滑块,其尺寸远小于L,它与木板之间的动摩擦因数μ=0.2,g=10m/s2,某时刻滑块m一水平向右的初速度v0=4m/s,从左端滑上木板的上表面,同时对木板施加一个水平向右的恒定拉力F.求:(1)若F=5N,求滑块从开始运动到距离木板左端最远处所需时间;
(2)若要使滑块不至于从木板上滑落,拉力F大小应满足的条件.
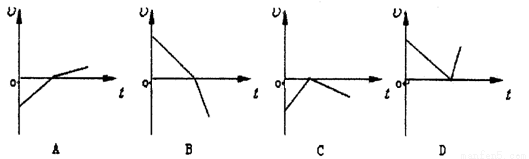
分析 (1)滑块相对于地做匀减速运动,木块相对于地做匀加速运动.开始阶段,A的速度大于车的速度,则A相对于车向右滑行,当两者速度相等后,A相对于车静止,则当两者速度相等时,滑块在小车上运动时相对小车滑行的最大距离.由牛顿第二定律求出加速度,然后应用匀变速直线运动的速度公式求出时间.
(2)要使滑块不从木块上滑落,是指既不能从木块的右端滑落,也不能从左端滑落.滑块不从右端滑落的临界条件是滑块到达木块的右端时,滑块与木块具有共同的速度,根据牛顿第二定律和运动学公式结合,以及速度相等的条件,可求出此时F,为F的最小值.滑块不从左端滑落的临界条件是滑块到达木块的左端时,滑块与木块具有共同的速度,可求出此时F的最大值,综合得到F的范围.
解答 解:(1)F施加的瞬间,由牛顿第二定律得:
滑块的加速度:a1=$\frac{μmg}{m}$=μg=2m/s2,
木块的加速度:a2=$\frac{F+μmg}{M}$=14m/s2,
滑块与木块速度相等时,滑块距离木块的左端距离最远,由匀变速直线运动的速度公式得:
v0-a1t=a2t,
代入数据解得:t=0.25s;
(2)滑块不滑落的临界条件是滑块到达木块的右端时,两者具有共同的速度v1,
则:$\frac{{v}_{0}^{2}-{v}_{1}^{2}}{2{a}_{1}}$=$\frac{{v}_{1}^{2}}{2{a}_{2}}$+L,
运动时间为:t=$\frac{{v}_{0}-{v}_{1}}{{a}_{1}}$=$\frac{{v}_{1}}{{a}_{2}}$,
代入数据解得:a2=6m/s2,
由牛顿第二定律得:F+-?mg=ma2,
代入数据解得:F=1N;
若F<1N,滑块滑到木块的右端时,速度仍大于木块的速度,于是将从木块上滑落,所以F必须大于等于1N.
当F较大时,在滑块到达木块的右端之前,就与木块具有相同的速度,之后,滑块必须相对木块静止,才不会从木块的左端滑落.
由牛顿第二定律得:F=(m+M)a,?mg=Ma,
解得:F=3N,
若F大于3N,滑块就会相对木块向左滑下.
综上:力F应满足的条件是:1N≤F≤3N.
答:(1)若F=5N,滑块从开始运动到距离木板左端最远处所需时间是0.25s;
(2)若要使滑块不至于从木板上滑落,拉力F大小应满足的条件是1N≤F≤3N.
点评 牛顿定律和运动公式结合是解决力学问题的基本方法,这类问题的基础是分析物体的受力情况和运动情况,难点在于分析临界状态,挖掘隐含的临界条件.

 如图所示,一带电粒子由O点垂直场强方向进入偏转电场,若初动能为Ek,射出电场时动能为2Ek,若初动能为4Ek,则射出电场时动能为(不计重力)( )
如图所示,一带电粒子由O点垂直场强方向进入偏转电场,若初动能为Ek,射出电场时动能为2Ek,若初动能为4Ek,则射出电场时动能为(不计重力)( )| A. | 3Ek | B. | 8Ek | C. | 4.25Ek | D. | 2.5Ek |
 如图所示,水平向右的匀强电场中有一绝缘斜面,一带电金属滑块以Ek0=30J的初动能从斜面底端A冲上斜面,到顶端B时返回,已知滑块从A滑到B的过程中克服摩擦力做功10J,克服重力做功24J,则( )
如图所示,水平向右的匀强电场中有一绝缘斜面,一带电金属滑块以Ek0=30J的初动能从斜面底端A冲上斜面,到顶端B时返回,已知滑块从A滑到B的过程中克服摩擦力做功10J,克服重力做功24J,则( )| A. | 滑块带正电,上滑过程中电势能减小4J | |
| B. | 滑块上滑过程中机械能增加4J | |
| C. | 滑块上滑到斜面中点时重力势能增加12J | |
| D. | 滑块返回到斜面底端时动能为15J |
 正弦交变电流经过匝数比为n1:n2=10:1的理想变压器与电阻R、交流电压表V、交流电流表A按图2甲所示方式连接,R=10Ω.图乙是R两端电压U随时间变化的图象,Um=10V,则下列说法中正确的是( )
正弦交变电流经过匝数比为n1:n2=10:1的理想变压器与电阻R、交流电压表V、交流电流表A按图2甲所示方式连接,R=10Ω.图乙是R两端电压U随时间变化的图象,Um=10V,则下列说法中正确的是( )| A. | 通过R的电流iR随时间t变化的规律是iR=$\sqrt{2}$cos100πt(A) | |
| B. | 电流表A的读数为0.1 A | |
| C. | 电流表A的读数为$\frac{\sqrt{2}}{20}$ A | |
| D. | 电压表V的读数为10 V |
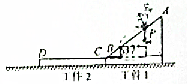 如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不连接)置于粗糙的水平面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度L=0.5m的粗糙水平面,CD与AB相较于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的摩擦动因数为μ1=0.5,P为AB上的一个确定点,质量m+0.2kg,可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6)
如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不连接)置于粗糙的水平面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度L=0.5m的粗糙水平面,CD与AB相较于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的摩擦动因数为μ1=0.5,P为AB上的一个确定点,质量m+0.2kg,可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6)