题目内容
6.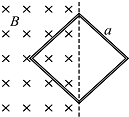 如图所示,一正方形线圈的匝数为n,边长为a,线圈平面与匀强磁场垂直,且一半处在磁场中.在△t时间内,磁感应强度的方向不变,大小由B均匀地增大到2B.在此过程中,线圈中的磁通量改变量大小△φ=$\frac{B{a}^{2}}{2}$,产生的感应电动势为E=$\frac{nB{a}^{2}}{2△t}$.
如图所示,一正方形线圈的匝数为n,边长为a,线圈平面与匀强磁场垂直,且一半处在磁场中.在△t时间内,磁感应强度的方向不变,大小由B均匀地增大到2B.在此过程中,线圈中的磁通量改变量大小△φ=$\frac{B{a}^{2}}{2}$,产生的感应电动势为E=$\frac{nB{a}^{2}}{2△t}$.
分析 根据法拉第电磁感应定律E=n$\frac{△∅}{△t}$=n$\frac{△B}{△t}$S,求解感应电动势,其中S是有效面积.
解答 解:在此过程中,线圈中的磁通量改变量大小△φ=$\frac{2B-B}{△t}$×$\frac{{a}^{2}}{2}$=$\frac{B{a}^{2}}{2}$
根据法拉第电磁感应定律E=n$\frac{△∅}{△t}$=n$\frac{△B}{△t}$S=$\frac{nB{a}^{2}}{2△t}$
故答案为:$\frac{B{a}^{2}}{2}$;$\frac{nB{a}^{2}}{2△t}$.
点评 解决电磁感应的问题,关键理解并掌握法拉第电磁感应定律E=n$\frac{△∅}{△t}$=n$\frac{△B}{△t}$S,知道S是有效面积,即有磁通量的线圈的面积.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
16.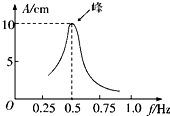 如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )
如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )
 如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )
如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )| A. | 摆长约为10cm | |
| B. | 摆长约为2m | |
| C. | 若增大摆长,共振曲线的“峰”将向左移动 | |
| D. | 若增大摆长,共振曲线的“峰”将向右移动 |
17.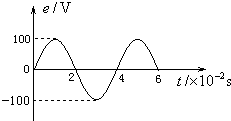 某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
 某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )| A. | 交变电流的周期为0.04s | B. | 电阻R两端的有效电压是100V | ||
| C. | 交变电流的有效值为1A | D. | 交变电流的最大值为1A |
11.如图2所示,物体受到水平推力F的作用,在粗糙水平面上做直线运动.监测到推力F、物体速度v随时间t变化的规律如图1所示.取g=10m/s2,则( )


| A. | 第1s内推力做功为1J | |
| B. | 第2s内推力F做功的平均功率$\overline{P}$=1.5W | |
| C. | 第1.5s时推力F的功率为2W | |
| D. | 第2s内物体克服摩擦力做的功W=2.0J |
16.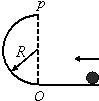 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列说法错误的是( )
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列说法错误的是( )
 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列说法错误的是( )
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列说法错误的是( )| A. | 小球落地点离O点的水平距离为$\sqrt{2}$R | |
| B. | 小球落地点时的动能为$\frac{5mgR}{2}$ | |
| C. | 小球落回水平面时重力的瞬时功率为mg•2$\sqrt{gR}$ | |
| D. | 若将半圆弧轨道上部的$\frac{1}{4}$圆弧截去,其他条件不变,则小球能达到的最大高度比P点高1.5R |

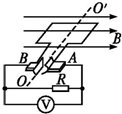 如图所示,匀强磁场的磁感应强度B=$\sqrt{2}$T,边长L=10cm的正方形线圈共100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2rad/s,外电路中的电阻R=4Ω,求:
如图所示,匀强磁场的磁感应强度B=$\sqrt{2}$T,边长L=10cm的正方形线圈共100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2rad/s,外电路中的电阻R=4Ω,求: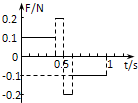 一质量为100g的质点处于静止状态,现受一个力的作用,其中的大小变化如图所示.在此过程中,求:
一质量为100g的质点处于静止状态,现受一个力的作用,其中的大小变化如图所示.在此过程中,求: