题目内容
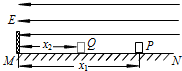如图所示，水平光滑绝缘轨道MN的左端有一个固定挡板，轨道所在空间存在E=4.0×102 N/C、水平向左的匀强电场．一个质量m=0.10kg、带电荷量q=5.0×10-5 C的滑块（可视为质点）从轨道上与挡板相距x1=0.20m的P点由静止释放，滑块在电场力作用下向左做匀加速直线运动．当滑块与挡板碰撞后，滑块沿轨道向右做匀减速直线运动，运动到与挡板相距x2=0.10m的Q点时，滑块第一次速度减为零．若滑块在运动过程中电荷量始终保持不变，求：（1）滑块沿轨道向左做匀加速直线运动的加速度的大小；
（2）滑块从P点运动到挡板处的过程中，电场力所做的功；
（3）滑块第一次与挡板碰撞过程中损失的机械能．
分析：（1）光滑绝缘的轨道没有摩擦力，滑块水平方向只受电场力作用，根据牛顿第二定律可以求出加速度的大小；
（2）根据功的定义，由滑块在水平方向的位移和电场力求得；
（3）根据功能关系，与挡板碰撞过程中损失的机械能等于电场力作P到Q对滑块所做的功．
（2）根据功的定义，由滑块在水平方向的位移和电场力求得；
（3）根据功能关系，与挡板碰撞过程中损失的机械能等于电场力作P到Q对滑块所做的功．
解答：解：（1）设滑块沿轨道向左做匀加速运动的加速度为a，此过程滑块所受合外力为
F=qE=2.0×10-2 N
根据牛顿第二定律有 F=ma
解得a=0.20m/s2．
（2）滑块从P点运动到挡板处的过程中，电场力所做的功
W1=qEx1=4.0×10-3 J．
（3）根据功能关系可知，滑块第一次与挡板碰撞过程中损失的机械能等于滑块由P点运动到Q点过程中电场力所做的功，即
△E=qE（x1-x2）=2.0×10-3 J．
答：
（1）滑块沿轨道向左做匀加速直线运动的加速度的大小为0.20 m/s2；
（2）滑块从P点运动到挡板处的过程中，电场力所做的功为4.0×10-3 J；
（3）滑块第一次与挡板碰撞过程中损失的机械能为2.0×10-3 J．
F=qE=2.0×10-2 N
根据牛顿第二定律有 F=ma
解得a=0.20m/s2．
（2）滑块从P点运动到挡板处的过程中，电场力所做的功
W1=qEx1=4.0×10-3 J．
（3）根据功能关系可知，滑块第一次与挡板碰撞过程中损失的机械能等于滑块由P点运动到Q点过程中电场力所做的功，即
△E=qE（x1-x2）=2.0×10-3 J．
答：
（1）滑块沿轨道向左做匀加速直线运动的加速度的大小为0.20 m/s2；
（2）滑块从P点运动到挡板处的过程中，电场力所做的功为4.0×10-3 J；
（3）滑块第一次与挡板碰撞过程中损失的机械能为2.0×10-3 J．
点评：本题运用功能关系求解分析滑块与挡板碰撞所损失的机械能△E，也可以根据动能定理分过程求解．
练习册系列答案
阅读快车系列答案
相关题目
[选做题]本题包括A、B、C三小题，请选定其中两题，并在相应的答题区域内作答．若三题都做，则按A、B两题评分．
的活塞密封了一定质量的空气，在活塞的上方竖直固定一支架，在支架的O点通过细线系一质量为
的球，球心到O点的距离为
．活塞与支架的总质量为
，已知当地的重力加速度
，大气压强
，气缸和活塞都是绝热的．现将细线拉直到水平，稳定后由静止释放球，当球第一次运动到最低点时，活塞下降了
且恰好速度为零，此时细线中的拉力为
．求球由静止释放到第一次运动到最低点的过程中气缸中的气体增加的内能
．
．（提示小球在达到最低点是机械能的减少等于汽缸中空气内能的增加） 
