题目内容
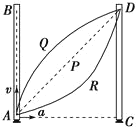
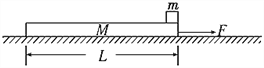
【题目】如图所示(俯视),MN和PQ是两根固定在同一水平面上的足够长且电阻不计的光滑平行金属导轨,两导轨间距为L=0.20m,其间有一个方向垂直水平面竖直向下的匀强磁场,磁感应强度B1=5.0T,导轨上NQ之间接一电阻R1=0.40Ω。质量为m2=0.2kg橡胶棒和阻值为R2=0.10Ω、质量为m1=0.4kg的金属杆垂直导轨放置并与导轨始终保持良好接触,两导轨右端通过金属导线分别与电容器C的两极板相连。电容器C的A极板开有小孔b,b正对固定、绝缘、薄壁弹性圆筒上的小孔a(只能容一个粒子通过),圆筒壁光滑,筒内有垂直水平面竖直向下的匀强磁场,磁感应强度B2=×10-3T,O是圆筒的圆心,圆筒的半径r=0.40m。
(1)橡胶棒以v0=10m/s的速度与静止的金属杆发生碰撞(时间极短),碰撞过程中系统动能损失一半。碰撞后立即对金属杆施加一个与导轨平行的水平向左的力F,使金属杆以碰撞后的速度做匀速运动,求F的大小;
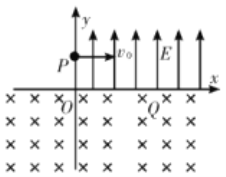
(2)当金属杆处于(2)问中的匀速运动状态时,电容器内紧靠B极板D处且静止的一个带正电的粒子经电容器C加速后由b孔射出,并从a孔垂直磁场B2并正对着圆心O进入筒中,该粒子与器壁碰撞后恰好又从小孔a射出圆筒而做周期性运动。已知该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,粒子的比荷为![]() =5×107(C/kg),求该带电粒子每次进磁场到出磁场过程中与圆筒壁碰撞的次数及所用的时间。(不计粒子重力及空气阻力)
=5×107(C/kg),求该带电粒子每次进磁场到出磁场过程中与圆筒壁碰撞的次数及所用的时间。(不计粒子重力及空气阻力)

【答案】(1)F=10N;(2)发生2次碰撞;![]()
【解析】
(1)由动量守恒得
m2v0=m1v1+m2v2
由能量守恒得
![]() m2v02=2
m2v02=2![]() (
(![]() m1v12+
m1v12+![]() m2v22)
m2v22)
得
v1=5m/s,v2=0
v1=![]() m/s ;v2=
m/s ;v2=![]() m/s不合理舍去
m/s不合理舍去
安培力F=B1IL,电流为
I=![]()
解得
F=10N
(2)设杆匀速运动时C两极板间的电压为U,带电粒子进入圆筒的速率为v、在磁场中作匀速圆周运动的半径为R,由于C与电阻R1并联,根据欧姆定得
U=IR1=4V
根据动能定理有
Uq=![]() mv2
mv2
带电粒子在磁场中作匀速圆周运动
![]()
由几何关系得
![]()
每段轨迹圆弧对应的圆心角为
![]()
粒子在圆筒内的轨迹具有对称性,在一个周期内与筒壁发生2次碰撞,由3段相同的圆弧组成
 或
或![]()

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案