题目内容
如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧BCD的B点相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,∠COB=θ,现有质量为m的小物体从距D点为
的地方无初速的释放,已知物体恰能从D点进入圆轨道.求:
(1)为使小物体不会从A点冲出斜面,小物体与斜面间的动摩擦因数至少为多少?
(2)若小物体与斜面间的动摩擦因数μ=
,则小物体在斜面上通过的总路程大小?
(3)小物体通过圆弧轨道最低点C时,对C的最大压力和最小压力各是多少?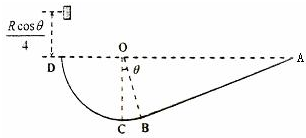
| Rcosθ |
| 4 |
(1)为使小物体不会从A点冲出斜面,小物体与斜面间的动摩擦因数至少为多少?
(2)若小物体与斜面间的动摩擦因数μ=
| sinθ |
| 2cosθ |
(3)小物体通过圆弧轨道最低点C时,对C的最大压力和最小压力各是多少?

(1)为使小物体不会从A点冲出斜面,由动能定理得mg
-μmgcosθ
=0
解得动摩擦因数至少为:μ=
(2)分析运动过程可得,最终小物体将从B点开始做往复的运动,由动能定理得
mg(
+Rcosθ)-μmgScosθ=0
解得小物体在斜面上通过的总路程为:S=
(3)由于小物体第一次通过最低点时速度最大,此时压力最大,由动能定理,得
mg(
+R)=
mv2
由牛顿第二定律,得
Nmax-mg=m
解得Nmax=3mg+
mgcosθ
最终小物体将从B点开始做往复的运动,则有
mgR(1-cosθ)=
mv′2
Nmin-mg=m
联立以上两式解得Nmin=mg(3-2cosθ)
由牛顿第三定律,得小物体通过圆弧轨道最低点C时对C的最大压力
Nmax′=3mg+
mgcosθ,
最小压力Nmin′=mg(3-2cosθ).
| Rcosθ |
| 4 |
| Rcosθ |
| sinθ |
解得动摩擦因数至少为:μ=
| sinθ |
| 4cosθ |
(2)分析运动过程可得,最终小物体将从B点开始做往复的运动,由动能定理得
mg(
| Rcosθ |
| 4 |
解得小物体在斜面上通过的总路程为:S=
| 5Rcosθ |
| 2sinθ |
(3)由于小物体第一次通过最低点时速度最大,此时压力最大,由动能定理,得
mg(
| Rcosθ |
| 4 |
| 1 |
| 2 |
由牛顿第二定律,得
Nmax-mg=m
| v2 |
| R |
解得Nmax=3mg+
| 1 |
| 2 |
最终小物体将从B点开始做往复的运动,则有
mgR(1-cosθ)=
| 1 |
| 2 |
Nmin-mg=m
| v′2 |
| R |
联立以上两式解得Nmin=mg(3-2cosθ)
由牛顿第三定律,得小物体通过圆弧轨道最低点C时对C的最大压力
Nmax′=3mg+
| 1 |
| 2 |
最小压力Nmin′=mg(3-2cosθ).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放有一小球C,A、B、C的质量均为m.给小球一水平向右的瞬时速度v0,使小球在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,初速度v0必须满足( )
如图所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放有一小球C,A、B、C的质量均为m.给小球一水平向右的瞬时速度v0,使小球在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起,初速度v0必须满足( ) 如图所示,竖直固定在地面上的轻弹簧的上端,连接一物体B,B上放一物体A,现用力F竖直向下压A、B的物体至某一位置静止,然后撤去力F,则在撤去F的瞬间( )
如图所示,竖直固定在地面上的轻弹簧的上端,连接一物体B,B上放一物体A,现用力F竖直向下压A、B的物体至某一位置静止,然后撤去力F,则在撤去F的瞬间( ) 如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )
如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )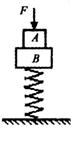
 如图所示,竖直固定在地面上的轻弹簧的上端,连接一物体B,B上放一物体A,现用力F竖直向下压A、B的物体至某一位置静止,然后撤去力F,则在撤去F的瞬间
如图所示,竖直固定在地面上的轻弹簧的上端,连接一物体B,B上放一物体A,现用力F竖直向下压A、B的物体至某一位置静止,然后撤去力F,则在撤去F的瞬间