题目内容
10. 如图所示,水平放置的平行金属轨相距L=0.05m,左端拉一电阻R=0.15Ω,磁感应强度B=0.4T的匀强磁场方向垂直于导轨平面,导体棒ab垂直放在寻轨上,并能无摩擦地沿导轨滑动,导体棒ab的电阻R0=0.05Ω,导轨的电阻忽略不计,当导体棒ab以v=4.0m/s的速度水平向右匀速滑动时,试问:
如图所示,水平放置的平行金属轨相距L=0.05m,左端拉一电阻R=0.15Ω,磁感应强度B=0.4T的匀强磁场方向垂直于导轨平面,导体棒ab垂直放在寻轨上,并能无摩擦地沿导轨滑动,导体棒ab的电阻R0=0.05Ω,导轨的电阻忽略不计,当导体棒ab以v=4.0m/s的速度水平向右匀速滑动时,试问:(1)导体棒ab上感应电流的方向和大小;
(2)维持导体棒ab做匀速直线运动,需要垂直作用于导体棒ab上的水平外力的大小和方向;
(3)水平外力做功的功率.
分析 (1)由法拉第电磁感应定律求ab棒产生的感应电动势;由右手定则判断回路中感应电流的方向,由欧姆定律求感应电流的大小;
(2)由平衡条件水平外力F的大小等于安培力大小,由安培力公式求出安培力大小即可,即可求得外力的大小,确定其方向;
(3)由公式P=Fv求解外力做功的功率.
解答 解:(1)根据法拉第电磁感应定律,知ab棒产生的感应电动势为:
E=BLv=0.4×0.05×4=0.08V
由右手定则可知,导体棒ab上感应电流的方向为b到a,感应电流大小为:
I=$\frac{E}{R+{R}_{0}}$=$\frac{0.08}{0.15+0.05}$A=0.4A
(2)根据左手定则可知ab棒所受的安培力F1水平向左,为维持ab棒做匀速运动,应添加一个与F1等值反向的水平外力F,所以外力的方向必须水平向右.
大小为:F=F1=BIL=0.4×0.4×0.05=0.008N
(3)水平外力做功的功率为:P=Fv=0.008×4W=0.032W
答:(1)导体棒ab上感应电流的方向由b到a,大小是0.4A;
(2)维持导体棒ab做匀速直线运动,需要垂直作用于导体棒ab上的水平外力的大小为0.008N,方向水平向右;
(3)水平外力做功的功率为0.032W.
点评 本题是电磁感应、电路和磁场知识的综合,关键要掌握法拉第电磁感应定律、欧姆定律、安培力公式等电磁感应的基本规律.

练习册系列答案
相关题目
20.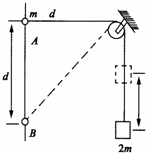 将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
 将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=$\frac{d}{2}$ | |
| B. | 环到达B处时,环与重物的速度大小之比为$\frac{\sqrt{2}}{2}$ | |
| C. | 环从A到B,环减少的机械能等于重物增加的机械能 | |
| D. | 环能下降的最大高度为$\frac{4d}{3}$ |
18.物体受到两个力F1和F2的作用,F1=6N,F2=9N,则它们的合力F的数值范围是( )
| A. | 6N≤F≤9N | B. | 3N≤F≤15N | C. | 3N≤F≤9N | D. | 6N≤F≤15N |
5.带电粒子M只在电场力作用下由P点运动到Q点,在此过程中克服电场力做了2.0×10-6J的功.那么( )
| A. | P点的场强一定小于Q点的场强 | |
| B. | P点的电势一定高于Q点电势 | |
| C. | M在P点的电势能一定小于它在Q点电势能 | |
| D. | M在P点的动能一定大于Q点的动能 |
15. 如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某初速度垂直左边界射入,穿过此区域的时间为t,若加上磁感应强度为B、垂直纸面向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出磁场时偏离原方向60°,利用以上数据可求出( )
如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某初速度垂直左边界射入,穿过此区域的时间为t,若加上磁感应强度为B、垂直纸面向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出磁场时偏离原方向60°,利用以上数据可求出( )
 如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某初速度垂直左边界射入,穿过此区域的时间为t,若加上磁感应强度为B、垂直纸面向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出磁场时偏离原方向60°,利用以上数据可求出( )
如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某初速度垂直左边界射入,穿过此区域的时间为t,若加上磁感应强度为B、垂直纸面向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出磁场时偏离原方向60°,利用以上数据可求出( )| A. | 带电粒子的比荷 | |
| B. | 带电粒子在磁场中运动的时间 | |
| C. | 带电粒子的初速度 | |
| D. | 带电粒子在磁场中做圆周运动的半径 |
2.某交流发电机线圈电阻为0.4Ω,给灯泡提供如图所示的正弦式交变电流.下列说法中正确的是( )


| A. | 交变电流的频率为0.02Hz | |
| B. | 交变电流的瞬时表达式为i=5cos50πt(A) | |
| C. | 在t=0.01s时,穿过交流发电机线圈的磁通量最大 | |
| D. | 发电机线圈产生的热功率为5W |
19. 如图所示,理想变压器的副线圈上接有两个相同的灯泡L1和L2,输电线的电阻忽略不计.当开关S断开时,灯泡L1正常发光.保持输入电压U1不变,当开关S接通时,下列说法中正确的是( )
如图所示,理想变压器的副线圈上接有两个相同的灯泡L1和L2,输电线的电阻忽略不计.当开关S断开时,灯泡L1正常发光.保持输入电压U1不变,当开关S接通时,下列说法中正确的是( )
 如图所示,理想变压器的副线圈上接有两个相同的灯泡L1和L2,输电线的电阻忽略不计.当开关S断开时,灯泡L1正常发光.保持输入电压U1不变,当开关S接通时,下列说法中正确的是( )
如图所示,理想变压器的副线圈上接有两个相同的灯泡L1和L2,输电线的电阻忽略不计.当开关S断开时,灯泡L1正常发光.保持输入电压U1不变,当开关S接通时,下列说法中正确的是( )| A. | 副线圈两端的输出电压U2减小 | B. | 副线圈中的电流I2减小 | ||
| C. | 原线圈中的电流I1增大 | D. | 原线圈的输入功率增大 |
 质量m=0.2kg的小球放在竖立的轻弹簧上,并把球往下按至A的位置,如图所示,迅速松手后,弹簧把球弹起,球升至最高位置C,途中经过位置B时弹簧正好处于自由状态.已知B、A的高度差x1=0.1m,C、B的高度差x2=0.2m,空气的阻力可忽略,重力加速度g=10m/s2,弹性势能的表达式Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量.求:
质量m=0.2kg的小球放在竖立的轻弹簧上,并把球往下按至A的位置,如图所示,迅速松手后,弹簧把球弹起,球升至最高位置C,途中经过位置B时弹簧正好处于自由状态.已知B、A的高度差x1=0.1m,C、B的高度差x2=0.2m,空气的阻力可忽略,重力加速度g=10m/s2,弹性势能的表达式Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量.求: 如图所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r=30cm处放置一小物块A,其质量为m=2kg,A与盘面间相互作用的静摩擦力的最大值为其重力的k倍(k=0.48),试求:
如图所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r=30cm处放置一小物块A,其质量为m=2kg,A与盘面间相互作用的静摩擦力的最大值为其重力的k倍(k=0.48),试求: