题目内容
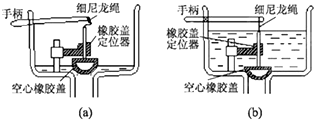
11. 如图所示,轻质弹簧一端固定,另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止释放后,经过B处速度最大,到达C处(AC=h)时速度减为零.若在此时给圆环一个竖直向上的速度v,它恰好能回到A点.弹簧始终在弹性限度内,重力加速度为g,则圆环( )
如图所示,轻质弹簧一端固定,另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止释放后,经过B处速度最大,到达C处(AC=h)时速度减为零.若在此时给圆环一个竖直向上的速度v,它恰好能回到A点.弹簧始终在弹性限度内,重力加速度为g,则圆环( )| A. | 下滑过程中,加速度一直增大 | |
| B. | 下滑过程中,克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| C. | 在C处弹簧的弹性势能为 mgh-$\frac{1}{4}$mv2 | |
| D. | 上下两次经过B点的速度大小相等 |
分析 根据圆环的运动情况分析下滑过程中,加速度的变化;
研究圆环从A处由静止开始下滑到C和在C处获得一竖直向上的速度v,恰好能回到A两个过程,运用动能定理列出等式求解;
研究圆环从A处由静止开始下滑到B过程和圆环从B处上滑到A的过程,运用动能定理列出等式
解答 解:A、圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,
所以圆环先做加速运动,再做减速运动,经过B处的速度最大,
所以经过B处的加速度为零,所以加速度先减小,后增大,故A错误
B、研究圆环从A处由静止开始下滑到C过程,运用动能定理列出等式
mgh-Wf-W弹=0-0=0
在C处获得一竖直向上的速度v,恰好能回到A,运用动能定理列出等式
-mgh+W弹-Wf=0-$\frac{1}{2}$mv2
解得:Wf=-$\frac{1}{4}$mv2,故B正确
C、W弹=$\frac{1}{4}$mv2-mgh,所以在C处,弹簧的弹性势能为mgh-$\frac{1}{4}$mv2,故C正确;
D、研究圆环从A处由静止开始下滑到B过程,运用动能定理列出等式
mgh′-W′f-W′弹=$\frac{1}{2}{mv}_{B}^{2}$-0
研究圆环从B处上滑到A的过程,运用动能定理列出等式
-mgh′-W′f+W′弹=0-$\frac{1}{2}{mv′}_{B}^{2}$
mgh′+W′f-W′弹=$\frac{1}{2}{mv′}_{B}^{2}$
由于W′f>0,所以$\frac{1}{2}{mv′}_{B}^{2}$>$\frac{1}{2}{mv}_{B}^{2}$,所以上滑经过B的速度大于下滑经过B的速度,故D错误
故选:BC
点评 能正确分析小球的受力情况和运动情况,对物理过程进行受力、运动、做功分析,是解决问题的根本方法,掌握动能定理的应用

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 1:3:5:7 | B. | 1:2:3:4 | C. | 12:22:32:42 | D. | 13:23:33:43 |
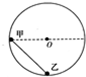 内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为R的轻杆,一端固定有质量为m的小球甲,另一端固定有质量为2m的小球乙,将两小球放入凹槽内小球乙位于凹槽的最低点,如图所示由静止释放后( )
内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为R的轻杆,一端固定有质量为m的小球甲,另一端固定有质量为2m的小球乙,将两小球放入凹槽内小球乙位于凹槽的最低点,如图所示由静止释放后( )| A. | 下滑过程中甲球减少的机械能总是等于乙球增加的机械能 | |
| B. | 下滑过程中甲球减少的重力势能总是等于乙球增加的重力势能 | |
| C. | 甲球可沿凹槽下滑到槽的最低点 | |
| D. | 杆从右向左滑回时,乙球一定能回到凹槽的最低点 |
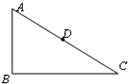 如图所示,D是斜面AC的中点,AD段和DC段分别由两种不同的材料构成.现有一小滑块(可视成质点)从斜面顶端A处由静止开始滑下,恰能滑到AC的底端C处静止.则关于滑块在斜面AC上的运动情况,下列说法正确的是( )
如图所示,D是斜面AC的中点,AD段和DC段分别由两种不同的材料构成.现有一小滑块(可视成质点)从斜面顶端A处由静止开始滑下,恰能滑到AC的底端C处静止.则关于滑块在斜面AC上的运动情况,下列说法正确的是( )| A. | 滑块在AD段运动的平均速率大于在DC段运动的平均速率 | |
| B. | 滑块在AD段和DC 段运动的加速度大小相等 | |
| C. | 滑块在AD段和DC 段运动中克服摩擦力做的功相等 | |
| D. | 滑块在AD段和DC 段运动中时间相等 |
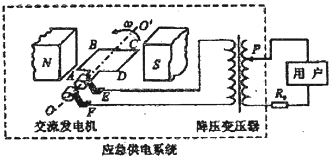
| A. | 用户得到的交变电压的频率为$\frac{ω}{2π}$ | |
| B. | 发电机线圈感应电动势的瞬时值表达式为e=NBωsinωt | |
| C. | 当发电机线圈处于图示位置时,原线圈两端的感应电动势最大 | |
| D. | 当用电器数目增多时,若要用电器两端电压保持不变,滑动触头P应向上滑动 |
| A. | 在B=0处,F一定等于零 | B. | 在F=0处,B一定等于零 | ||
| C. | 在B=1T,I=1A,l=1m时,F一定等于1N | D. | 若I=1A,l=1m,F=1N,B不一定等于1T |
 如图xoy平面为光滑水平面,现有一长为d宽为L的线框MNPQ在外力F作用下,沿x轴正方向以速度v做匀速直线运动,空间存在竖直方向的磁场,磁感应强度B=2B0cos$\frac{π}{d}$x(式中B0为已知量),规定竖直向下方向为磁感应强度正方向,线框电阻为R,t=0时刻MN边恰好在y轴处,则下列说法正确的是( )
如图xoy平面为光滑水平面,现有一长为d宽为L的线框MNPQ在外力F作用下,沿x轴正方向以速度v做匀速直线运动,空间存在竖直方向的磁场,磁感应强度B=2B0cos$\frac{π}{d}$x(式中B0为已知量),规定竖直向下方向为磁感应强度正方向,线框电阻为R,t=0时刻MN边恰好在y轴处,则下列说法正确的是( )| A. | 外力F为恒力 | |
| B. | t=0时,外力大小F=16B02L2$\frac{v}{R}$ | |
| C. | 通过线圈的瞬时电流I=$\frac{{4{B_0}Lvcos\frac{πvt}{d}}}{R}$ | |
| D. | 经过t=$\frac{d}{v}$,线圈中产生的电热Q=$\frac{2{{B}_{0}}^{2}{L}^{2}vd}{R}$ |