题目内容
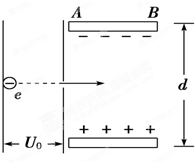
如图所示,有一电子(电量为e,质量为m,)经电压U
0加速后,进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且恰好能从金属板右缘飞出,求:
(1)该电子刚飞离加速电场时的速度大小
(2)金属板AB的长度.
(3)电子最后穿出电场时的动能.
分析:(1)电子先在加速电场中加速,由动能定理可求其加速后的速度,
(2)电子进入偏转电场中做类平抛运动,由于电子正好能穿过电场,所以在偏转电场中的偏转的距离就是
,由此可以求得极板的长度;
(3)电子正好能穿过电场偏转电场对电子做功
解答:解:(1)设电子被加速后速度大小为v
0,对于电子在加速电场中由动能定理得:
eU0=m ①
所以
v0= ②
(2)在偏转电场中,由电子做类平抛运动,设加速度为a,极板长度为L,由于电子恰好射出电场,所以有:
a== ③
L=v
0t ④
=at2 ⑤
由②③④⑤解得:
L=d(3)电子正好能穿过电场偏转电场,偏转的距离就是
,由此对电子做功
=EK-m ⑤
①代人⑤中得:
EK=eU0+e=e(U0+)答:(1)电子进入偏转电场时的速度为
v0=;(2)极板的长度为
L=d;(3)电子最后穿出电场时的动能
e(U0+).
点评:电子先在加速电场中做匀加速直线运动,后在偏转电场中做类平抛运动,根据电子的运动的规律逐个分析即可
练习册系列答案
相关题目
 如图所示,有一电子(电量为e,质量为m,)经电压U0加速后,进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且恰好能从金属板右缘飞出,求:
如图所示,有一电子(电量为e,质量为m,)经电压U0加速后,进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且恰好能从金属板右缘飞出,求:
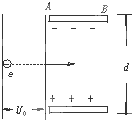 如图所示,有一电子(电量为e)经电压U0加速后,进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且正好能穿过电场,求:
如图所示,有一电子(电量为e)经电压U0加速后,进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且正好能穿过电场,求: 如图所示,有一电子经电压U0加速后,进入两块间距为d,电压为U的平行金属板间,若电子从两板正中间射入,且正好能穿出电场,金属板的长度为
如图所示,有一电子经电压U0加速后,进入两块间距为d,电压为U的平行金属板间,若电子从两板正中间射入,且正好能穿出电场,金属板的长度为 如图所示,有一电子在A点从静止开始经电压U0=1.8×103V加速后,进入两块间距为d=8cm,电压为U=900V的两平行金属板间,若电子从两板正中间射入,且恰好能穿出电场,若电子质量m=9.0×10-30kg,电量e=1.6×10-19C,电子所受重力忽略不计,求:
如图所示,有一电子在A点从静止开始经电压U0=1.8×103V加速后,进入两块间距为d=8cm,电压为U=900V的两平行金属板间,若电子从两板正中间射入,且恰好能穿出电场,若电子质量m=9.0×10-30kg,电量e=1.6×10-19C,电子所受重力忽略不计,求: