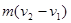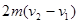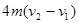题目内容
如图所示，弧形轨道与水平轨道平滑连接，轨道每处都是光滑的，且水平部分足够长.质量为m1的A球由静止从弧形轨道滑下，在水平轨道与质量为m2的B球发生弹性对心碰撞.要使两球能发生第二次碰撞，两球质量应满足怎样的关系？
m2>3 m1.
：设碰撞前A球速度为v，碰撞后速度分别为v1、v2，由动量守恒定律，
m1v= m1 v1+ m2v2，
由能量守恒定律，
m1v2=m1 v12+m2v22，
联立解得：v1=
v，
V2=
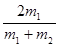v，
能够发生第二次相碰的条件是：- v1> v2
解得：m2>3 m1.
m1v= m1 v1+ m2v2，
由能量守恒定律，
m1v2=m1 v12+m2v22，联立解得：v1=
v，V2=
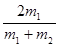v，能够发生第二次相碰的条件是：- v1> v2
解得：m2>3 m1.
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
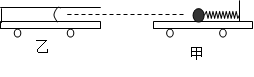
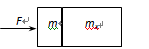
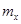应为
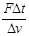
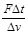
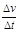就越大，且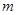
的物体上，在时间
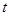内物体速度由
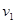变为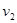
，则力2F作用在质量为
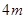的物体上，在时间
