题目内容
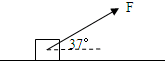 如图,质量为m=4.6千克的物体静置于水平面上,物体与水平面的滑动摩擦系数为0.2,现用与水平方向成θ=37°角的斜向上力F拉物体,为使物体沿水平面匀速运动5米.求:
如图,质量为m=4.6千克的物体静置于水平面上,物体与水平面的滑动摩擦系数为0.2,现用与水平方向成θ=37°角的斜向上力F拉物体,为使物体沿水平面匀速运动5米.求:(1)拉力F应为多大?
(2)拉力F对物体做的功是多少?
(3)匀速运动时如果速度为2米/秒,撤去F后还能滑动多远?
分析:(1)对物体进行受力分析,根据匀速运动平衡求拉力F的大小;
(2)根据功的定义式W=FLcosα求力F的功;
(3)撤去力F后,在摩擦力作用下物体做匀减速直线运动,摩擦力做的功等于物体动能的变化,由此求解即可.
(2)根据功的定义式W=FLcosα求力F的功;
(3)撤去力F后,在摩擦力作用下物体做匀减速直线运动,摩擦力做的功等于物体动能的变化,由此求解即可.
解答:解:(1)建立如图坐标系对物体进行受力分析有:
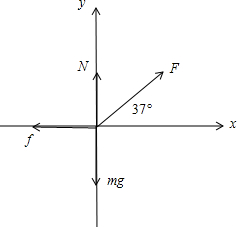
根据物体平衡有:
F合x=Fcos37°-f=0 ①
F合y=N+Fsin37°-mg=0 ②
f=μN ③
由①②③解得:F=10N
(2)根据功的定义有力F在物体产生5m的位移中对物体做功
W=FLcos37°=10×5×0.8=40J
(3)当撤去力F后,物体所受摩擦力f′=μN′=μmg=9.2N
根据动能定理有:-f′x=0-
mv2得
位移x=
=
m=1m
答:(1)拉力F应为10N;
(2)拉力F对物体做的功是40J;
(3)匀速运动时如果速度为2米/秒,撤去F后还能滑动1m.

根据物体平衡有:
F合x=Fcos37°-f=0 ①
F合y=N+Fsin37°-mg=0 ②
f=μN ③
由①②③解得:F=10N
(2)根据功的定义有力F在物体产生5m的位移中对物体做功
W=FLcos37°=10×5×0.8=40J
(3)当撤去力F后,物体所受摩擦力f′=μN′=μmg=9.2N
根据动能定理有:-f′x=0-
| 1 |
| 2 |
位移x=
| ||
| f′ |
| ||
| 9.2 |
答:(1)拉力F应为10N;
(2)拉力F对物体做的功是40J;
(3)匀速运动时如果速度为2米/秒,撤去F后还能滑动1m.
点评:正确分析物体的受力是解决本题的关键,注意摩擦力f与正压力成正比,不一定与重力成正比.

练习册系列答案
相关题目
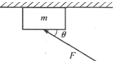 如图,质量为m的木块,在斜向左上方的力F的作用下,沿天花板向左作匀速直线运动,则该物体受到的作用力的个数为( )
如图,质量为m的木块,在斜向左上方的力F的作用下,沿天花板向左作匀速直线运动,则该物体受到的作用力的个数为( )| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,质量为m的物体,在已知恒定水平拉力F作用下,以速度v1开始沿水平向右运动,经位移s后速度变为v2.已知物体与水平面的摩擦力恒为f,加速度为a.现在根据牛顿第二定律和运动学公式推导出,合外力对物体所做功与物体动能变化的关系.物体速度由v1到v2的过程中,请用题目给出的物理量,写出基本的物理公式,完成填空.
如图,质量为m的物体,在已知恒定水平拉力F作用下,以速度v1开始沿水平向右运动,经位移s后速度变为v2.已知物体与水平面的摩擦力恒为f,加速度为a.现在根据牛顿第二定律和运动学公式推导出,合外力对物体所做功与物体动能变化的关系.物体速度由v1到v2的过程中,请用题目给出的物理量,写出基本的物理公式,完成填空.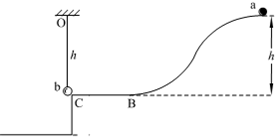 (1)以下说法正确的是
(1)以下说法正确的是