题目内容
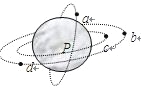
【题目】如图所示,三个同心圆将空间分隔成四个区域,圆I的半径为R;圆II的半径为2R,在圆I与圆Ⅱ间的环形区域内存在垂直于纸面向外的磁感应强度为B的匀强磁场;圆III是一绝缘圆柱形管,半径为4R,在圆Ⅱ与圆III间存在垂直于纸面向里的匀强磁场B1。在圆心O处有一粒子源,该粒子源可向各个方向射出速率相同、质量为m、带电荷量为q的粒子,粒子重力不计。假设粒子每一次经过圆Ⅱ且与该圆相切时均进入另一磁场。粒子源所射出的粒子刚好沿圆II的切线方向进入匀强磁场B1。
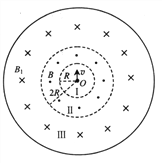
(1)求粒子的速度大小;
(2)若进入匀强磁场B1的粒子刚好垂直打在圆III的管壁上,求B1的大小(可用B表示);
(3)若打在圆III管壁上的粒子能原速率反弹,求粒子从O点开始到第一次回到O点所经历的时间。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)粒子运动轨迹如图:
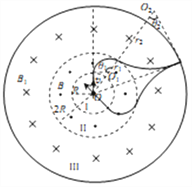
由牛顿定律可得: ![]()
由几何关系可知: ![]()
解得: ![]()
(2)由牛顿第二定律: ![]()
由几何关系可知: ![]()
解得: ![]()
(3)由几何关系可得:圆心角:θ1=1270
圆心角:θ2=530
粒子运动的第一段圆弧长: ![]()
粒子运动的第二段圆弧长: ![]()
由几何关系知粒子第一次回到O点运动的时间: ![]()
解得: ![]()

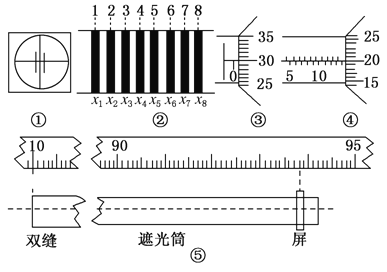
【题目】某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为97.50 cm,摆球直径为2.00 cm,然后用秒表记录了单摆振动50次所用的时间,如图所示,则:
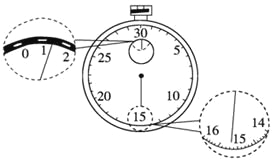
(1)该摆摆长为______cm,秒表所示读数为______s.
(2)如果测得的g值偏小,可能的原因是( )
A.测摆线长时摆线拉得过紧 |
B.摆线上端悬点未固定,振动中出现松动,使摆线长度增加了 |
C.开始计时时,秒表过迟按下 |
D.实验中误将49次全振动记为50次 |
(3)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l与T的数据,再以l为横坐标,T2为纵坐标,将所得数据连成直线如图所示,并求得该直线的斜率为k,则重力加速度g=______(用k表示).