题目内容
1.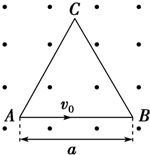 如图所示,ABC为与匀强磁场垂直的边长为a的等边三角形,磁场垂直纸面向外,荷质比为$\frac{e}{m}$的电子以速度v0从A点沿AB方向射入,欲使电子能经过BC边,则磁感应强度B的取值范围.
如图所示,ABC为与匀强磁场垂直的边长为a的等边三角形,磁场垂直纸面向外,荷质比为$\frac{e}{m}$的电子以速度v0从A点沿AB方向射入,欲使电子能经过BC边,则磁感应强度B的取值范围.
分析 电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出磁感应强度的临界值,然后分析答题.
解答 解:当电子从C点离开磁场时,电子做匀速圆周运动对应的半径最小,设为R,
则几何知识得:2Rcos30°=a,解得:R=$\frac{a}{\sqrt{3}}$;
欲使电子能经过BC边,必须满足:R>$\frac{a}{\sqrt{3}}$,
而R=$\frac{m{v}_{0}}{eB}$,所以$\frac{m{v}_{0}}{eB}$>$\frac{a}{\sqrt{3}}$,
解得:B<$\frac{\sqrt{3}m{v}_{0}}{ae}$;
答:磁感应强度B的取值范围是:B<$\frac{\sqrt{3}m{v}_{0}}{ae}$.
点评 本题是磁场中临界条件问题,关键是运用几何知识求最小的轨迹半径,即可由半径求解B的范围.

练习册系列答案
相关题目
11.关于磁极间的相互作用,下列说法正确的是( )
| A. | 同名磁极相吸引 | B. | 同名磁极相排斥 | ||
| C. | 异名磁极相排斥 | D. | 以上说法均不正确 |
12.一物体由静止开始以恒定加速度下落,经过时间1s落至地面,落地时速度是9m/s.下列说法中正确的是( )
| A. | 物体下落高度为5 m | B. | 物体下落高度为4.9 m | ||
| C. | 物体下落的加速度为9 m/s2 | D. | 物体下落的加速度为9.8 m/s2 |
6.关于磁感强度,下列说法中正确的是( )
| A. | 磁感强度的大小反映了磁场的强弱 | |
| B. | 磁感强度是描述磁场强弱和方向的物理量 | |
| C. | 磁感强度的方向就是通电导线在磁场中所受作用力的方向 | |
| D. | 磁感强度的方向就是小磁针在其中N极的受力方向 |
13.一船以恒定的速率渡河,且水流速度恒定,要使船垂直到达对岸,则( )
| A. | 船不可能沿直线到达对岸 | B. | 此种方式渡河时间最短 | ||
| C. | 船应垂直河岸航行 | D. | 船的航行方向应偏向上游一侧 |
10.现已建成的核电站发电的能量来自于( )
| A. | 化学反应放出的能量 | B. | 人工放射性同位素放出的能量 | ||
| C. | 重核裂变放出的能量 | D. | 轻核聚变放出的能量 |
 如图所示,有一个不透明的长方体形状的筒,高16cm,底面边长12cm,其中盛满某种液体,有人在筒前某处向筒内观察,恰好看到筒内侧的最低点,若把液体倒出,筒放在原处,人仍在原处向筒内观察,则只能看到顶部以下9cm处,求液体的折射率和光在液体中的传播速度.
如图所示,有一个不透明的长方体形状的筒,高16cm,底面边长12cm,其中盛满某种液体,有人在筒前某处向筒内观察,恰好看到筒内侧的最低点,若把液体倒出,筒放在原处,人仍在原处向筒内观察,则只能看到顶部以下9cm处,求液体的折射率和光在液体中的传播速度.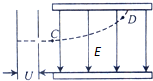 如图所示一个初速度为零的电子通过电压为U的电场加速后,从C点垂直于场强为E的匀强电场方向射入两平行板之间,电子到达该电场中另一点D时,电子的速度大小为v.设电子的电量为e、质量为m.求:
如图所示一个初速度为零的电子通过电压为U的电场加速后,从C点垂直于场强为E的匀强电场方向射入两平行板之间,电子到达该电场中另一点D时,电子的速度大小为v.设电子的电量为e、质量为m.求: