题目内容
（12分）如下图所示，让摆球从图中的C位置由静止开始摆下，摆到最低点D处，摆线刚好被拉断，小球在粗糙的水平面上由D点向右做匀减速运动，到达小孔A进入半径R=0.3m的竖直放置的光滑圆弧轨道，当摆球进入圆轨道立即关闭A孔.已知摆线长L=2m，兹=60°，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2.试求：
（1）求摆线能承受的最大拉力为多大？
（2）要使摆球能进入圆轨道并且不脱离轨道，求粗糙水平面摩擦因数滋的范围.
（1）当摆球由C到D运动机械能守恒：mg(L-Lcos兹)=
mvD2(1分)
由牛顿第二定律可得：Fm-mg=m
（1分）
可得：Fm =2mg=10N(1分)
（2）小球不脱圆轨道分两种情况：①要保证小球能达到A孔，设小球到达A孔的速度恰好为零，由动能定理可得：-滋1mgs=0-mvD2（1分）
可得：滋1=0.5（1分）
若进入A孔的速度较小，那么将会在圆心以下做等幅摆动，不脱离轨道.其临界情况为到达圆心等高处速度为零，
由机械能守恒可得： mvA2=mgR（1分）
由动能定理可得：-滋2mgs= mvA2-mvD2（1分）
可求得：滋2=0.35（1分）
②若小球能过圆轨道的最高点则不会脱离轨道，在圆周的最高点由牛顿第二定律可得：mg=m
（1分）
由动能定理可得：-滋3mgs-2mgR= mv2-mvD2（1分）
解得：滋3=0.125（1分）
综上所以摩擦因数滋的范围为：0.35≤滋≤0.5或者滋≤0.125（1分）
解析:略
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
，
）
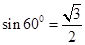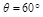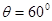，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2。试求：
，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2。试求：
，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2。试求：