题目内容
1.如图1所示,两根粗糙、足够长的直金属导轨MN、PQ彼此平行,与水平面夹角为θ,导轨间距为L,金属导轨上单位长度的电阻阻值为r;M、P两点间接有一电源,电动势为E,内阻不计,其中MP与导轨垂直,M、P间导线的电阻忽略不计.一根质量为m、电阻不计的直金属杆放在两导轨上,并与导轨垂直,且处处与导轨接触良好.整套装置处于磁感应强度大小为B,方向垂直斜面向下的匀强磁场中,重力加速度为g.
(1)若金属杆放在导轨上某位置时,恰好不受导轨的摩擦力而静止,求该位置到MP的距离:
(2)若金属杆只能放在如图1中导轨ab、cd之间才能保持静止,且a、b分别为cM、dP的中点,求导轨ac长度的电阻.(已知没有磁场时,金属杆不能自由静止在导轨上)
分析 (1)金属杆恰好不受导轨的摩擦力而静止时,受到重力、导轨的支持力和安培力而平衡,由平衡条件和安培力公式求出导轨的电阻,从而得到该位置到MP的距离.
(2)金属杆只能放在如图1中导轨ab、cd之间才能保持静止,说明在cd处刚好不下滑,在ab处刚好不上滑,根据平衡条件求解.
(3)求出金属棒刚好不上滑和刚好不下滑时所受的安培力,再求出电流的范围,得到电阻的范围.
解答 解:(1)设该位置到MP的距离为x.
金属杆恰好不受导轨的摩擦力而静止时,有 mgsinθ=BIL,I=$\frac{E}{2xr}$
联立得 x=$\frac{BLE}{2mgrsinθ}$
(2)设导轨ac长度的电阻为R′,最大静摩擦力为f.
据题:ab棒在cd处刚好不下滑,则有 mgsinθ=B$\frac{E}{4R′}$L+f
在ab处刚好不上滑,则有 mgsinθ+f=B$\frac{E}{2R′}$L
联立解得 R′=$\frac{3BLE}{8mgsinθ}$,f=$\frac{1}{3}$mgsinθ
答:
(1)该位置到MP的距离为 $\frac{BLE}{2mgrsinθ}$.
(2)导轨ac长度的电阻为$\frac{3BLE}{8mgsinθ}$.
点评 对于通电导体在磁场中平衡问题,关键要正确分析受力情况,把握导体棒刚好滑动的临界条件:静摩擦力达到最大,由平衡条件和安培力公式研究.

练习册系列答案
相关题目
17. 如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )
如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )
 如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )
如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )| A. | A、B两点间的电势差一定等于$\frac{mgLsinθ}{q}$ | |
| B. | 小球在B点的电势能一定大于在A点的电势能 | |
| C. | 若该电场是匀强电场,则其电场强度的最大值一定为$\frac{mg}{q}$ | |
| D. | 若该电场是由斜面上方某位置的点电荷产生的,则该点电荷一定为负点电荷,且处于斜面中点的正上方 |
18.关于力、运动状态及惯性的说法,下列正确的是( )
| A. | 牛顿最早指出力不是维持物体运动的原因 | |
| B. | 笛卡尔对牛顿第一定律的建立做出了贡献 | |
| C. | 一个运动的物体,如果不再受力了,它总会逐渐停下来,这说明,静止状态才是物体长时间不受力时的“自然状态 | |
| D. | 车速越大,刹车后滑行的路程越长,所以惯性越大 |
6. 如所示,图中实线是一簇未标明方向的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,根据此图能做出正确的判断的是( )
如所示,图中实线是一簇未标明方向的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,根据此图能做出正确的判断的是( )
 如所示,图中实线是一簇未标明方向的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,根据此图能做出正确的判断的是( )
如所示,图中实线是一簇未标明方向的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,根据此图能做出正确的判断的是( )| A. | 带电粒子所带电荷的正负 | |
| B. | 带电粒子在a、b两点受力方向 | |
| C. | 带电粒子在a、b两点加速度何处较大 | |
| D. | 带电粒子在a、b两点的场强的方向 |
11.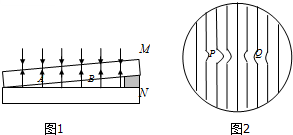 如图1所示用单色光检查工件上表面是否平整,观察到的现象如图所示的条纹中的P和Q分别为待测工件在A和B处的情况,这说明( )
如图1所示用单色光检查工件上表面是否平整,观察到的现象如图所示的条纹中的P和Q分别为待测工件在A和B处的情况,这说明( )
 如图1所示用单色光检查工件上表面是否平整,观察到的现象如图所示的条纹中的P和Q分别为待测工件在A和B处的情况,这说明( )
如图1所示用单色光检查工件上表面是否平整,观察到的现象如图所示的条纹中的P和Q分别为待测工件在A和B处的情况,这说明( )| A. | M为待测工件 | |
| B. | N的上表面B处向上凹陷 | |
| C. | M的上表面A处向下凹陷 | |
| D. | 若减小二工件间空气膜夹角,则条纹间距变密 |
 如图所示,设质量为m、电荷量为q的带电粒子以初速度v0沿垂直于电场线的方向,进入长为l、间距为d、电压为U的平行金属板间的匀强电场中.若不计粒子的重力,求如下的物理量:
如图所示,设质量为m、电荷量为q的带电粒子以初速度v0沿垂直于电场线的方向,进入长为l、间距为d、电压为U的平行金属板间的匀强电场中.若不计粒子的重力,求如下的物理量: 如图所示,质量M=1kg的木板B静止在水平面上,一质量m=1kg的滑块A以v0=10m/s的水平初速度从左端滑上木板B,最终停止在木板B上,滑块A与木板B间的动摩擦因数μ1=0.4,木板B与水平面间的动摩擦因数μ2=0.15,g=10m/s2,求:
如图所示,质量M=1kg的木板B静止在水平面上,一质量m=1kg的滑块A以v0=10m/s的水平初速度从左端滑上木板B,最终停止在木板B上,滑块A与木板B间的动摩擦因数μ1=0.4,木板B与水平面间的动摩擦因数μ2=0.15,g=10m/s2,求: