题目内容
1.假设地球和火星均为球体且均不考虑它们自转的影响,已知火星的质量约为地球质量的0.1倍,火星的半径约为地球半径的0.5倍,则火星上的第一宇宙速度与地球上的第一宇宙速度之比约为( )| A. | $\frac{1}{5}$ | B. | 5 | C. | $\frac{\sqrt{5}}{5}$ | D. | $\sqrt{5}$ |
分析 根据万有引力提供向心力得到第一宇宙速度公式,带入质量和半径关系可得比值.
解答 解:由万有引力提供向心力可知:
F向心力=F引=G$\frac{Mm}{{R}^{2}}$=m$\frac{{V}^{2}}{R}$
得第一宇宙速度为:V=$\sqrt{\frac{GM}{R}}$
得:V火:V地=$\sqrt{\frac{0.1M×R}{M×0.5R}}$=$\sqrt{\frac{1}{5}}$=$\frac{\sqrt{5}}{5}$,故C正确,ABD错误;
故选:C.
点评 第一宇宙速度是卫星贴近星球表面飞行时的最大运行速度,环绕半径正好为星球半径.

练习册系列答案
相关题目
12.一质量为2kg的质点在如图甲所示的xOy平面内运动,在x方向的速度-时间(vx-t)图象和y方向的位移-时间(y-t)图象分别如图乙、丙所示,由此可知( )


| A. | t=0s时,质点的速度大小为12m/s | B. | 质点做加速度恒定的曲线运动 | ||
| C. | 前两秒,质点所受的合力大小为10N | D. | t=1.0s时,质点的速度大小为7m/s |
9.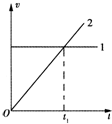 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )| A. | 图线2表示竖直分运动的v-t图线 | |
| B. | t1时刻的速度方向与初速度方向夹角为30° | |
| C. | t1时间内的竖直位移与水平位移之比为$\frac{1}{2}$ | |
| D. | 2t1时刻的速度方向与初速度方向夹角为60° |
10. 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )| A. | $\frac{{{r}_{1}}^{2}{ω}^{2}}{{r}_{3}}$ | B. | $\frac{{{r}_{3}}^{2}{ω}^{2}}{{{r}_{1}}^{2}}$ | C. | $\frac{{{r}_{3}}^{3}{ω}^{2}}{{{r}_{1}}^{2}}$ | D. | $\frac{{r}_{1}{r}_{2}{ω}^{2}}{{r}_{3}}$ |
16. 一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )
一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )
 一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )
一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )| A. | 两列波相遇后,各自独立传播 | |
| B. | 两列波同时传播到P点 | |
| C. | 波源S1,S2的起振方向相反 | |
| D. | 两列波相遇过程中,P点振幅可达(A1+A2) |
 如图所示,单摆摆长L=1.0m,C点在悬点O的正下方,D点与C点相距为x=0.6m,C、D之间是光滑绝缘水平面,当摆球A(不带电)运动至左侧最大位移处时,带电小球B从D点由静止释放,小球B的电荷量q=+2.0×10-2C.A、B的质量均为m=200g.当小球B运动到C点时,A、B小球恰在C点迎面相碰.(A、B小球均看成质点,不计空气阻力,计算时取g=10m/s2,π2=10).求
如图所示,单摆摆长L=1.0m,C点在悬点O的正下方,D点与C点相距为x=0.6m,C、D之间是光滑绝缘水平面,当摆球A(不带电)运动至左侧最大位移处时,带电小球B从D点由静止释放,小球B的电荷量q=+2.0×10-2C.A、B的质量均为m=200g.当小球B运动到C点时,A、B小球恰在C点迎面相碰.(A、B小球均看成质点,不计空气阻力,计算时取g=10m/s2,π2=10).求 如图所示,质量为0.4kg的木块以2m/s的速度水平地滑上静止的平板小车,车的质量为1.6kg,木块与小车之间的摩擦系数为0.2(g取10m/s2).设小车足够长,求:
如图所示,质量为0.4kg的木块以2m/s的速度水平地滑上静止的平板小车,车的质量为1.6kg,木块与小车之间的摩擦系数为0.2(g取10m/s2).设小车足够长,求: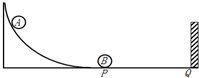 如图所示,质量为0.3kg的小球A放在光滑的曲面上,离地面的高度0.2m,小球B静止在水平地面上,B离竖直墙的距离是PQ=3.5m,A静止释放,与B发生弹性碰撞,B与墙碰撞无机械能损失,也不计B与墙碰撞时间,在离墙2.5m处两球发生第二次碰撞,重力加速度g=10m/s2,求:
如图所示,质量为0.3kg的小球A放在光滑的曲面上,离地面的高度0.2m,小球B静止在水平地面上,B离竖直墙的距离是PQ=3.5m,A静止释放,与B发生弹性碰撞,B与墙碰撞无机械能损失,也不计B与墙碰撞时间,在离墙2.5m处两球发生第二次碰撞,重力加速度g=10m/s2,求: