题目内容
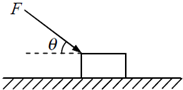
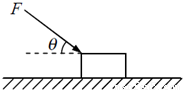
（A）如图所示，放在水平面上的物体质量m=2kg，受到一个斜向下的与水平方向成q=37°角的推力F=10N的作用，从静止开始运动．已知物体与水平面间的动摩擦因数m=0.25，sin37°=0.6，cos37°=0.8，g取10m/s2．问：（1）物体l0s末的速度是多大？物体l0s内的位移是多少？
（2）若10s末撤去推力，物体在水平面上运动的总位移是多少？
分析：（1）对物体受力分析，根据牛顿第二定律求出物体的加速度，再根据速度和位移公式分别求出10s末物体的速度大小和位移大小．
（2）根据牛顿第二定律求出撤去外力时物块的加速度，再结合运动学公式总位移大小．
（2）根据牛顿第二定律求出撤去外力时物块的加速度，再结合运动学公式总位移大小．
解答：解：（1）物体受力如图所示，据牛顿第二定律有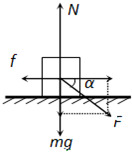
竖直方向上 N-mg-Fsinα=0
水平方向上 Fcosα-f=ma
又 f=μN
联立解得，a=0.75m/s2
物体l0s末的速度是v=at=0.75×10=7.5m/s
位移为x=
at2=37.5m
（2）撤去力F后，据牛顿第二定律有-f′=ma′
N′-mg=0
又f′=μN′
解得 a′=-μg=-2.5m/s2
减速运动的位移为x′=
=11.25m
所以总位移为x总=x+x′=48.75m
答：
（1）物体l0s末的速度是7.5m/s，物体l0s内的位移是37.5m．
（2）若10s末撤去推力，物体在水平面上运动的总位移是48.75m．
竖直方向上 N-mg-Fsinα=0
水平方向上 Fcosα-f=ma
又 f=μN
联立解得，a=0.75m/s2
物体l0s末的速度是v=at=0.75×10=7.5m/s
位移为x=
| 1 |
| 2 |
（2）撤去力F后，据牛顿第二定律有-f′=ma′
N′-mg=0
又f′=μN′
解得 a′=-μg=-2.5m/s2
减速运动的位移为x′=
| 0-v2 |
| 2a′ |
所以总位移为x总=x+x′=48.75m
答：
（1）物体l0s末的速度是7.5m/s，物体l0s内的位移是37.5m．
（2）若10s末撤去推力，物体在水平面上运动的总位移是48.75m．
点评：解决本题的关键理清物体的运动规律，结合牛顿第二定律和运动学公式进行求解．
练习册系列答案
相关题目
如图所示，放在水平面上的物体受到一个斜向上的拉力作用，但物体仍保持静止状态，现将F分解为水平方向的力F1和竖直向上的力F2，下列说法正确的是（ ）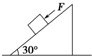
如图所示，放在斜面上的物体处于静止状态，斜面倾角为30°，物体质量为m，若想使物体沿斜面从静止开始下滑，至少需要施加平行斜面向下的推力F=0.2mg，则（ ）
