题目内容
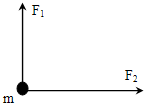质量为2kg的质点同时受到相互垂直的两个力F1，F2的作用，如图所示，其中F1=3N，F2=4N，求质点的加速度大小和方向．分析：根据牛顿第二定律，质点的加速度与合外力成正比，与物体的质量成反比，方向与合外力的方向相同，即a=
．
| F合 |
| m |
解答：解：如图所示：
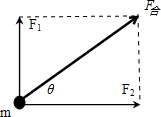根据力的平行四边形定则，可知质点所受F1和F2的合力大小为：
F合=
=5N
F合与水平方向的夹角θ满足tanθ=
=
∴θ=37°
根据牛顿第二定律，质点产生的加速度为：
a=
=
m/s2=2.5m/s2，方向与水平方向成37°角．
答：质点产生的加速度为2.5m/s2，方向与水平方向成37°角．
根据力的平行四边形定则，可知质点所受F1和F2的合力大小为：F合=
|
F合与水平方向的夹角θ满足tanθ=
| F1 |
| F2 |
| 3 |
| 4 |
∴θ=37°
根据牛顿第二定律，质点产生的加速度为：
a=
| F合 |
| m |
| 5 |
| 2 |
答：质点产生的加速度为2.5m/s2，方向与水平方向成37°角．
点评：能用平行四边形定则求质点所受的合力大小和方向，能根据牛顿第二定律求出加速度的大小和方向．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
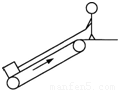
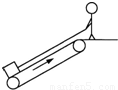
（2011?金华二模）传送带以恒定速度v=4m/s顺时针运行，传送带与水平面的夹角θ=37°．现将质量m=2kg的小物品轻放在其底端（小物品可看成质点），平台上的人通过一根轻绳用恒力F=20N拉小物品，经过一段时间物品被拉到离地高为H=1.8m的平台上，如图所示．已知物品与传送带这间的动摩擦因数μ=0.5，设最大静摩擦力等于滑动摩擦力，g取10m/s2，已知sin37°=0.6，cos37°=0.8．求：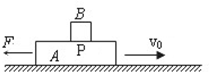
如图所示，木板A长L=6m，质量为M=8kg，在水平面上向右做直线运动．某时刻木板A速度vo=6m/s，在此时刻对木板A施加一个方向水平向左的恒力F=32N，与此同时，将一个质量m=2kg的小物块B轻放在木板A上的P点（小物块可视为质点，放在P点时相对于地面的速度为零），P点到木板A右端距离为lm，木板A与地面间的动摩擦因数为0.16，其他摩擦均不计．取g=10m/s2．求：
=37°。现将质量m=2kg的小物品轻放在其底端（小物品可看成质点），平台上的人通过一根轻绳用恒力F=20N拉小物品，经过一段时间物品被拉到离地高为H=1.8m的平台上，如图所示。已知物品与传送带之间的动摩擦因数
=0.5，设最大静摩擦力等于滑动摩擦力，g取l0m／s2，已知sin37°=0.6，cos37°=0,8。求：
