题目内容
15．小强和小勇在水平面上同一地点，小强以初速度vo沿与水平方向成θ角斜向上抛出一小球，与此同时小勇沿抛出方向奔跑，欲能接住该球，关于小勇的运动（不计空气阻力），以下说法正确的是（ ）（其中sin2θ=2sinθcosθ）| A． | 小勇的平均速度为vosinθ | B． | 小勇的平均速度为vocosθ | ||
| C． | 小勇运动的时间为$\frac{{{v_o}sinθ}}{g}$ | D． | 小勇运动的时间为2vo2sin2θ |
分析 将小球的运动分解为水平和竖直两个方向，根据竖直方向上的竖直上抛运动和水平方向的匀速直线运动可求得运动时间及平均速度．
解答 解：将球的运动分解为水平和竖直方向的运动；竖直方向做竖直上抛运动，vy=v0sinθ；在空中运动时间t=2$\frac{{v}_{y}}{g}$=$\frac{2{v}_{0}sinθ}{g}$；
因小勇当好接住球，故小勇运动时间为t；运动位移为小球的水平位移x=v0cosθt=$\frac{2{v}_{0}cosθsinθ}{g}$，则小勇的平均速度$\overline{v}$=$\frac{x}{t}$=v0sinθ；故A正确，BCD错误；
故选：A．
点评 本题考查抛体运动规律，要注意明确解决抛体运动的方法为运动的合成与分解．
练习册系列答案
相关题目
如图所示，光滑水平地面静止放着质量m=10kg的木箱，与水平方向成θ=60°的恒力F作用于物体，恒力F=2.0N．当木箱在力F作用下由静止开始运动4.0s，求：
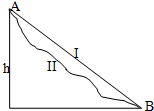
10．如图所示，若物体分别沿不同的路径Ⅰ和Ⅱ，从A运动B，则（ ）
| A． | 沿路径Ⅱ重力所做的功最大 | |
| B． | 沿路径Ⅰ和Ⅱ重力所做的功一样大 | |
| C． | 沿路径Ⅰ重力所做的功最大 | |
| D． | 由于路径Ⅱ是曲面无法判断其重力做功的多少 |
7．
一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系，进行了如下实验：在离地面高度为h的光滑水平桌面上，沿着与桌子边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的一个小钢球接触．当弹簧处于自然长度时，小钢球恰好在桌子边缘，如图所示．让钢球向左压缩弹簧一段距离后由静止释放，使钢球沿水平方向射出桌面，小钢球在空中飞行后落在水平地面上，水平距离为s．
（1）小刚球离开桌面时的速度大小为v=s$\sqrt{\frac{g}{2h}}$，弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式为Ep=$\frac{mg{s}^{2}}{4h}$．
（2）弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如表所示：
由实验数据，可确定弹性势能Ep与弹簧的压缩量x的关系为C（式中k为比例系数）
（A）Ep=kx （B）Ep=k$\sqrt{x}$ （C）Ep=kx2 （D）Ep=k$\frac{1}{x}$．
一个同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系，进行了如下实验：在离地面高度为h的光滑水平桌面上，沿着与桌子边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的一个小钢球接触．当弹簧处于自然长度时，小钢球恰好在桌子边缘，如图所示．让钢球向左压缩弹簧一段距离后由静止释放，使钢球沿水平方向射出桌面，小钢球在空中飞行后落在水平地面上，水平距离为s．（1）小刚球离开桌面时的速度大小为v=s$\sqrt{\frac{g}{2h}}$，弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式为Ep=$\frac{mg{s}^{2}}{4h}$．
（2）弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如表所示：
| 弹簧的压缩量x （cm） | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小钢球飞行的水平距离s （m） | 2.01 | 3.00 | 4.01 | 4.96 | 6.01 | 7.00 |
（A）Ep=kx （B）Ep=k$\sqrt{x}$ （C）Ep=kx2 （D）Ep=k$\frac{1}{x}$．
在真空中O点放一个点电荷Q=+1.0×10-9C，直线MN通过O点，OM的距离r=30cm，如图所示，求：（k=9.0×109Nm2/C2）求：
如图所示，半径R=0.4m的半圆轨道处于竖直平面内，半圆与水平地面切于圆的端点A，一质量为m=0.1kg的小球，以一定的初速度在水平地面上向左运动后，恰好能到达半圆轨道的最高点B点，最后小球落在C点．（取重力加速度g=10m/s2）．求：小球落在C点的动能．