题目内容
5. 如图所示,长度都为L=0.4m的两根细绳,一端系着同一个小球A,另一端分别系于相同高度的两点上,两绳间的夹角为α=120°,现使小球A在竖直平面上(垂直纸面)做小角度的摆动,当小球A经过最低位置的瞬间,另一小球B从A的正上方h高处自由落下,经过一段时间后击中A球,则h的可能值为( )
如图所示,长度都为L=0.4m的两根细绳,一端系着同一个小球A,另一端分别系于相同高度的两点上,两绳间的夹角为α=120°,现使小球A在竖直平面上(垂直纸面)做小角度的摆动,当小球A经过最低位置的瞬间,另一小球B从A的正上方h高处自由落下,经过一段时间后击中A球,则h的可能值为( )| A. | 0.1π2m | B. | 0.2π2m | C. | 0.3π2m | D. | 0.4π2m |
分析 给小球A一垂直于纸面向外的初速度v0,使小球垂直于纸面开始做小角度的摆动,求出等效摆长的大小,根据单摆的周期公式求出周期的大小,结合单摆的周期性求出 小球B下落的时间,从而得出高度的表达式.
解答 解:小球A的等效摆长L0=Lsin30°=0.2m,根据T=$2π\sqrt{\frac{{L}_{0}}{g}}$得,单摆的周期T=$2π\sqrt{0.02}s$,
单摆回到最低点的时间$t=\frac{nT}{2}$,
则h=$\frac{1}{2}g{t}^{2}=\frac{1}{2}g\frac{{n}^{2}{T}^{2}}{4}=\frac{{n}^{2}g{T}^{2}}{8}$,(n=1,2,3,…)
当n=1时,h=0.1π2,当n=2时,h=0.4π2,故A、D正确,B、C错误.
故选:AD.
点评 解决本题的关键通过等效替代法得出等效摆长的大小,通过单摆的周期公式进行求解.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
15.如图所示,在原来不带电的金属细杆ab附近P处,放置一个正点电荷,达到静电平衡后( )
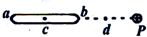
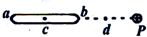
| A. | a端的电势比b端的高 | B. | a端的电势比b点的低 | ||
| C. | a端的电势比d点的低 | D. | c处场强不为零 |
16.关于匀速圆周运动,下列说法正确的是( )
| A. | 匀速圆周运动就是匀速运动 | B. | 匀速圆周运动是变速运动 | ||
| C. | 角速度越大,周期一定越小 | D. | 线速度越大,周期一定越小 |
20. 一带负电的试探电荷在不同电场中由静止释放,只受电场力作用,且沿直线运动,它运动的v-t图象如图中甲、乙所示,则下列关于试探电荷所处的电场说法正确的是( )
一带负电的试探电荷在不同电场中由静止释放,只受电场力作用,且沿直线运动,它运动的v-t图象如图中甲、乙所示,则下列关于试探电荷所处的电场说法正确的是( )
 一带负电的试探电荷在不同电场中由静止释放,只受电场力作用,且沿直线运动,它运动的v-t图象如图中甲、乙所示,则下列关于试探电荷所处的电场说法正确的是( )
一带负电的试探电荷在不同电场中由静止释放,只受电场力作用,且沿直线运动,它运动的v-t图象如图中甲、乙所示,则下列关于试探电荷所处的电场说法正确的是( )| A. | 甲图可能是在带正电的点电荷形成的电场中的v-t运动图象 | |
| B. | 甲图可能是在带负电的点电荷形成的电场中的v-t运动图象 | |
| C. | 乙图可能是在等量同种点电荷形成的电场中的v-t运动图象 | |
| D. | 乙图可能是在等量异种点电荷形成的电场中的v-t运动图象 |
10. 一列横波沿x轴正方向传播,在t=0时刻的波形曲线如图所示.已知这列波的质点P连续出现两次波峰的时间间隔为0.4s,则( )
一列横波沿x轴正方向传播,在t=0时刻的波形曲线如图所示.已知这列波的质点P连续出现两次波峰的时间间隔为0.4s,则( )
 一列横波沿x轴正方向传播,在t=0时刻的波形曲线如图所示.已知这列波的质点P连续出现两次波峰的时间间隔为0.4s,则( )
一列横波沿x轴正方向传播,在t=0时刻的波形曲线如图所示.已知这列波的质点P连续出现两次波峰的时间间隔为0.4s,则( )| A. | 这列波的波长为5 m | |
| B. | 这列波的传播速度为10 m/s | |
| C. | 当t=0.7 s时,质点Q第一次到达波峰 | |
| D. | 质点Q到达波峰时,质点P恰好到达波谷 |
7.一人用力踢质量为10kg的皮球,使球由静止以20m/s的速度飞出.假定人踢球瞬间对球平均作用力是200N,球在水平方向运动了20m停止.那么人对球所做的功为( )
| A. | 4000 J | B. | 2000 J | C. | 500 J | D. | 4 000 J |
