题目内容
18.已知月球绕地球公转的周期为T,它们绕地球的公转均可看作匀速圆周运动,并且公转轨道半径为r,则根据以上条件可确定( )| A. | 地球的质量 | B. | 月球的质量 | C. | 地球的体积 | D. | 月球的密度 |
分析 根据万有引力提供向心力求解中心天体(地球)的质量,由于不知道地球半径,所以无法求解地球体积.
解答 解:A、月球绕地球公转,做匀速圆周运动,根据万有引力提供向心力得$\frac{GMm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$则有:M=$\frac{4{π}^{2}{r}^{3}}{{GT}^{2}}$,可求出地球的质量,故A正确;
B、月球的质量在公式中约去,所以不能求出月球质量,故B错误;
C、由于不知道地球半径,所以无法求解地球体积,故C错误;
D、由于不知道月球质量和体积,所以无法求解月球密度,故D错误.
故选:A
点评 解决本题的关键掌握万有引力提供向心力公式的直接应用,注意公转半径不是地球或者月球的半径,而是两个球心之间的距离,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.关于第一宇宙速度,下列说法正确的是( )
| A. | 它是人造地球卫星绕地球作匀速圆周运动的最大速度 | |
| B. | 它是人造地球卫星在圆形轨道上的最小运行速度 | |
| C. | 它是能使卫星绕地球运行的最小环绕速度 | |
| D. | 它是人造卫星绕地球作椭圆轨道运行时在近地点的速度 |
6.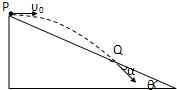 如图所示,从倾角为θ的足够长的斜面顶端P点以速度υ0抛出一个小球,落在斜面上Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变成2υ0,下列说法正确的是( )
如图所示,从倾角为θ的足够长的斜面顶端P点以速度υ0抛出一个小球,落在斜面上Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变成2υ0,下列说法正确的是( )
 如图所示,从倾角为θ的足够长的斜面顶端P点以速度υ0抛出一个小球,落在斜面上Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变成2υ0,下列说法正确的是( )
如图所示,从倾角为θ的足够长的斜面顶端P点以速度υ0抛出一个小球,落在斜面上Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变成2υ0,下列说法正确的是( )| A. | 由于抛出点不变,空中运动时间不变 | |
| B. | 由于水平速度变大,α角将变小 | |
| C. | 水平位移将大于原来的2倍,PQ也将大于原来的2倍 | |
| D. | 夹角α与初速度大小无关 |
13.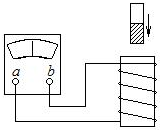 某同学用如图所示装置研究感应电流的方向与引起感应电流的磁场的关系.已知电流从a接线柱流入电流表时,电流表指针右偏.实验时,磁场方向、磁铁运动情况及电流表指针偏转情况都记录在表中.
某同学用如图所示装置研究感应电流的方向与引起感应电流的磁场的关系.已知电流从a接线柱流入电流表时,电流表指针右偏.实验时,磁场方向、磁铁运动情况及电流表指针偏转情况都记录在表中.
根据上表中记录的实验现象,由实验1、3得出的结论是穿过闭合电路的磁通量增加时,感应电流的磁场方向与原磁场方向相反.并由此回答下面二个问题:
(1)由实验2、4得出的结论是穿过闭合电路的磁通量减小时,感应电流的磁场方向与原磁场方向相同
(2)由实验1、2、3、4得出的结论是感应电流的磁场总是阻碍引起感应电流的磁通量的变化.
 某同学用如图所示装置研究感应电流的方向与引起感应电流的磁场的关系.已知电流从a接线柱流入电流表时,电流表指针右偏.实验时,磁场方向、磁铁运动情况及电流表指针偏转情况都记录在表中.
某同学用如图所示装置研究感应电流的方向与引起感应电流的磁场的关系.已知电流从a接线柱流入电流表时,电流表指针右偏.实验时,磁场方向、磁铁运动情况及电流表指针偏转情况都记录在表中.| 实验序号 | 磁场方向 | 磁铁运动情况 | 指针偏转情况 |
| 1 | 向下 | 插入 | 右偏 |
| 2 | 向下 | 拔出 | 左偏 |
| 3 | 向上 | 插入 | 左偏 |
| 4 | 向上 | 拔出 | 右偏 |
(1)由实验2、4得出的结论是穿过闭合电路的磁通量减小时,感应电流的磁场方向与原磁场方向相同
(2)由实验1、2、3、4得出的结论是感应电流的磁场总是阻碍引起感应电流的磁通量的变化.
10.质量为m的汽车,发动机的额定功率是P,欲开上一倾角为θ的斜面,受到的摩擦阻力为车重的K倍,那么汽车上坡的最大速度为( )
| A. | $\frac{P}{mgsinθ}$ | B. | $\frac{Pcosθ}{Kmg}$ | C. | $\frac{P}{{mg({K+sinθ})}}$ | D. | $\frac{Pcosθ}{{mg({K+sinθ})}}$ |
8. 据《天文学与天体物理学》报道,在地球的北半球就可以观测到距离地球1.3万光年的鹿豹座星团中两颗恒星,如图所示,它是由两颗大质量恒星构成的双星系统.该系统的两颗恒星质量分别为太阳的38倍和32倍,轨道周期为28小时,现两恒星外表面已开始接触,若已知太阳质量,引力常量,两星体可视为质量分布均匀的球体,则( )
据《天文学与天体物理学》报道,在地球的北半球就可以观测到距离地球1.3万光年的鹿豹座星团中两颗恒星,如图所示,它是由两颗大质量恒星构成的双星系统.该系统的两颗恒星质量分别为太阳的38倍和32倍,轨道周期为28小时,现两恒星外表面已开始接触,若已知太阳质量,引力常量,两星体可视为质量分布均匀的球体,则( )
 据《天文学与天体物理学》报道,在地球的北半球就可以观测到距离地球1.3万光年的鹿豹座星团中两颗恒星,如图所示,它是由两颗大质量恒星构成的双星系统.该系统的两颗恒星质量分别为太阳的38倍和32倍,轨道周期为28小时,现两恒星外表面已开始接触,若已知太阳质量,引力常量,两星体可视为质量分布均匀的球体,则( )
据《天文学与天体物理学》报道,在地球的北半球就可以观测到距离地球1.3万光年的鹿豹座星团中两颗恒星,如图所示,它是由两颗大质量恒星构成的双星系统.该系统的两颗恒星质量分别为太阳的38倍和32倍,轨道周期为28小时,现两恒星外表面已开始接触,若已知太阳质量,引力常量,两星体可视为质量分布均匀的球体,则( )| A. | 可求出两星球球心之间的距离 | |
| B. | 不可能求出两星球中任何一个的半径 | |
| C. | 可求出两星球中任何一个的密度 | |
| D. | 不可能求出两星球中任何一个的线速度 |

 两物体的质量分别为m和3m,滑轮的质量和摩擦都不计,质量为3m的物体离地面的高度为H,从静止开始释放,
两物体的质量分别为m和3m,滑轮的质量和摩擦都不计,质量为3m的物体离地面的高度为H,从静止开始释放,