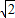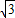题目内容
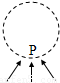
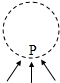
如图,圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以同样的速率通过P 点进入磁场.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的
.将磁感应强度的大小从原来的B1 变为 B2,结果相应的弧长变为原来的一半,则
等于( )
| 1 |
| 3 |
| B2 |
| B1 |
| A.2 | B.3 | C.
| D.
|

设圆的半径为r
(1)磁感应强度为B1时,从P点射入的粒子与磁场边界的最远交点为M,最远的点是轨迹上直径与磁场边界圆的交点,∠POM=120°,如图所示:
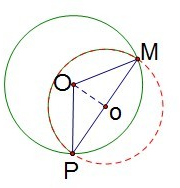
所以粒子做圆周运动的半径R为:sin60°=
,得:R=
磁感应强度为B2时,从P点射入的粒子与磁场边界的最远交点为N,最远的点是轨迹上直径与磁场边界圆的交点,∠PON=60°,如图所示:
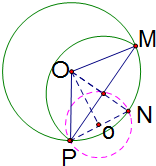
所以粒子做圆周运动的半径R′为:sin30°=
,得:R′=
由带电粒子做圆周运动的半径:R=
得:
R=
=
=
①
R′=
=
=
②
得:
=
;即:
=
故选D
(1)磁感应强度为B1时,从P点射入的粒子与磁场边界的最远交点为M,最远的点是轨迹上直径与磁场边界圆的交点,∠POM=120°,如图所示:

所以粒子做圆周运动的半径R为:sin60°=
| R |
| r |
| ||
| 2 |
磁感应强度为B2时,从P点射入的粒子与磁场边界的最远交点为N,最远的点是轨迹上直径与磁场边界圆的交点,∠PON=60°,如图所示:

所以粒子做圆周运动的半径R′为:sin30°=
| R′ |
| r |
| r |
| 2 |
由带电粒子做圆周运动的半径:R=
| mv |
| qB |
R=
| mv |
| qB |
| mv |
| qB1 |
| ||
| 2 |
R′=
| mv |
| qB |
| mv |
| qB2 |
| r |
| 2 |
| ① |
| ② |
| B1 |
| B2 |
| 1 | ||
|
| B2 |
| B1 |
| 3 |
故选D

练习册系列答案
相关题目
 如图,圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以同样的速率通过P 点进入磁场.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的
如图,圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以同样的速率通过P 点进入磁场.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的 如图,圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以相同的速率通过P点进入磁场.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的
如图,圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以相同的速率通过P点进入磁场.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的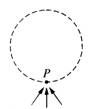
 B.
B. 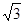 C.
2 D. 3
C.
2 D. 3 .将磁感应强度的大小从原来的B1 变为 B2,结果相应的弧长变为原来的一半,则
.将磁感应强度的大小从原来的B1 变为 B2,结果相应的弧长变为原来的一半,则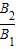 等于( )
等于( )