Question

遥控电动赛车的比赛中有一个规定项目是“飞跃壕沟”，如图所示，比赛中要求赛车从起点出发，沿水平直轨道运动，在B点飞出后跃过“壕沟”，落在平台EF段。已知赛车的质量m=1.0kg、额定功率P=10.0 W、在水平直轨道上受到的阻力恒为f=2. 0 N, BE的高度差h=0. 45 m,BE的水平距离x=0. 90 m。赛车车长不计，空气阻力不计，g取10m/s²。

(1)若赛车在水平直轨道上能达到最大速度，求最大速度v_m的大小;

(2)要跃过壕沟，求赛车在B点最小速度v的大小;

(3)比赛中，若赛车在A点达到最大速度v_m后即刻停止通电，赛车恰好能跃过壕沟，求AB段距离s。

 

Answer 1

【答案】

（1）5m/s（2）3m/s（3）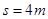

【解析】

试题分析：（1）赛车在水平轨道上达到最大速度时，设其牵引力为，根据牛顿第二定律有：

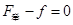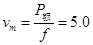  ①又   ②解得 m/s 

（2）赛车通过B点后做平抛运动，设在空中运动时间为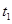，则有：  ③    ④

解得：m/s

（3）停止通电后，赛车在水平方向上只受阻力作用，

根据动能定理可得

代入数据解得：

考点：牛顿第二定律 ，平抛运动，动能定理