Question

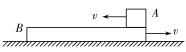
【题目】如图，水平光滑的地面上有A、B、C三个可视为质点的木块，质量分别为1 kg、6kg、6kg.木块A的左侧有一半径R=0.2 m的固定的光滑半圆弧轨道，一开始B、C处于静止状态，B、C之间的弹簧处于原长．给木块A一个水平向右的初速度，大小为v1=8 m/s，与木块B碰撞后，A被反弹，速度大小变为v2=4 m/s.(重力加速度g取10 m/s2)求：

（1）A过圆弧轨道的最高点时受到轨道的压力；

（2）弹簧具有的最大弹性势能．

Answer 1

【答案】（1）30N（2）6J

【解析】

(1)木块A从最低点到最高点的过程，由动能定理得

－mAg·2R=mAvA2－mAv22

最高点有F+mAg=mA

得：F=30N

（2）根据动量守恒定律得mAv1=mBvB－mAv2

解得vB=2 m/s

弹簧压缩至最短时，B、C速度相同，有mBvB=(mB＋mC)v

解得v=1 m/s

弹簧具有的最大弹性势能Ep=mBvB2－(mB＋mC)v2

得：Ep=6J