题目内容
9.某次实验所用打点计时器交流电的频率为50Hz,纸带的记录如图所示,图中前几个点模糊,因此从A点开始每打五个点取一个计数点,其中B、C、D、E 点的对应速度 vB=0.25 m/s,v C=0.33 m/s,vD=0.40 m/s,vE=0.48 m/s,由此推得F点的速度 vF=0.56 m/s.
分析 从A点开始每打五个点取一个计数点,所以每两个点间的时间间隔T为0.1s.求某点的瞬时速度时只需要找平均速度代替即可,如果找不出的,如:F点的,可用公式v=v0+at求解.
解答 解:某点的瞬时速度时只需要找平均速度代替:
vB=$\frac{{x}_{AC}}{2T}=\frac{(6.45-1.40)×1{0}^{-2}}{2×0.1}$=0.25m/s
vC=$\frac{{x}_{BD}}{2T}$=$\frac{(10.10-3.55)×1{0}^{-2}}{2×0.1}$=0.33m/s;
vD=$\frac{{x}_{CE}}{2T}=\frac{(14.50-6.45)×1{0}^{-2}}{2×0.1}=0.40m/s$
vE=$\frac{{x}_{DF}}{2T}=\frac{(19.65-10.10)×1{0}^{-2}}{2×0.1}=0.48m/s$
因为:vE-vD=0.08m/s;vD-vB=0.15m/s≈2×(vE-vD)且B到D的时间是D到E时间的2倍,所以物体的运动应该是匀加速直线运动.
由:a=$\frac{{v}_{E}-{v}_{D}}{T}得:$a=$\frac{0.08}{0.1}=0.8m/{s}^{2}$
由:vF=vE+aT得:
vF=0.48+0.8×0.1=0.56m/s
故答案为:0.25;0.33;0.40;0.48;0.56
点评 本题考查纸带的处理求速度的方法;处理纸带求某点瞬时速度时:首先选择找个平均速度来替代,实在找不到就用v=v0+at来求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下表是通过测量得到的一辆摩托车沿直线加速运动时速度随时间的变化.
请根据测量数据:
(1)画出摩托车运动的v-t图象.
(2)求摩托车在第一个10s内的加速度.
(3)根据画出的v-t图象,利用求斜率的方法求出第一个10s内的加速度,并与上面计算的结果进行比较.
(4)求摩托车在最后15s内的加速度.
| t/s | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| v/(m•s-1) | 0 | 10 | 20 | 30 | 20 | 10 | 0 |
(1)画出摩托车运动的v-t图象.
(2)求摩托车在第一个10s内的加速度.
(3)根据画出的v-t图象,利用求斜率的方法求出第一个10s内的加速度,并与上面计算的结果进行比较.
(4)求摩托车在最后15s内的加速度.
4.某物体运动的v-t图象如图所示,下列说法中不正确的是( )


| A. | 物体在第1 s末运动方向发生变化 | |
| B. | 物体在第2 s内和第3 s内的加速度是相同的 | |
| C. | 物体在4 s末返回出发点 | |
| D. | 物体在5 s末离出发点最远,且最大位移为0.5 m |
14.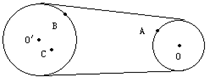 如图所示的皮带轮动装置,皮带轮O和O′上有三点A、B、C,OA=O′C=r,O′B=2r,则皮带轮转动时,A、B、C三点的运动情况有下列四种说法,正确的是( )
如图所示的皮带轮动装置,皮带轮O和O′上有三点A、B、C,OA=O′C=r,O′B=2r,则皮带轮转动时,A、B、C三点的运动情况有下列四种说法,正确的是( )
①vA=vB ②vB=vC ③ωA=ωB ④ωB=ωC.
 如图所示的皮带轮动装置,皮带轮O和O′上有三点A、B、C,OA=O′C=r,O′B=2r,则皮带轮转动时,A、B、C三点的运动情况有下列四种说法,正确的是( )
如图所示的皮带轮动装置,皮带轮O和O′上有三点A、B、C,OA=O′C=r,O′B=2r,则皮带轮转动时,A、B、C三点的运动情况有下列四种说法,正确的是( ) ①vA=vB ②vB=vC ③ωA=ωB ④ωB=ωC.
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
1. 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )
 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则此时( )| A. | 物块B的质量满足m2gsinθ=kd | |
| B. | 物块A的加速度为$\frac{F-kd}{m_1}$ | |
| C. | 拉力做功的瞬时功率为Fv | |
| D. | 此过程中,弹簧弹性势能的增量为Fd-m1dgsinθ-$\frac{1}{2}$m1v2 |
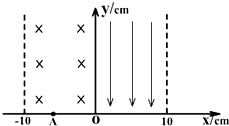 如图,在xoy平面内第二象限-10cm≤x区域内有垂直纸面向内的匀强磁场B,其大小为0.2T,在A(-6cm,0)点有一粒子发射源,向x轴上方180°范围内发射v=2.0×107m/s的负粒子,粒子的比荷为2.0×109C/kg,不计粒子重力,求:
如图,在xoy平面内第二象限-10cm≤x区域内有垂直纸面向内的匀强磁场B,其大小为0.2T,在A(-6cm,0)点有一粒子发射源,向x轴上方180°范围内发射v=2.0×107m/s的负粒子,粒子的比荷为2.0×109C/kg,不计粒子重力,求: 如图所示,把一个倾角为θ的光滑绝缘斜面固定在匀强电场中,电场方向水平向右,有一质量为m、带电量为+q的物体以初速度v0从A端滑上斜面恰好沿斜面匀速运动,求匀强电场的电场强度的大小.(重力加速度取g)
如图所示,把一个倾角为θ的光滑绝缘斜面固定在匀强电场中,电场方向水平向右,有一质量为m、带电量为+q的物体以初速度v0从A端滑上斜面恰好沿斜面匀速运动,求匀强电场的电场强度的大小.(重力加速度取g)