Question

（2008?南通一模）如图所示，由红、紫两种单色光组成的光束a，以入射角i从平行玻璃板上表面O点入射．已知平行玻璃板厚度为d，红光和紫光的折射率分别为n₁和n₂，真空中的光速为c，试求：
①红光在玻璃中传播的速度；
②红光和紫光在下表面出射点之间的距离．

Answer 1

分析：（1）由公式v=

c

n

求解红光在玻璃中传播的速度；
（2）由折射定律分别求出红光与紫光的折射角，由几何知识求解红光和紫光在下表面出射点之间的距离．

解答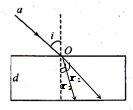：解：①红光在玻璃中传播的速度为：v=

c

n1

．
②设红光的折射角为r₁，紫光的折射角为r₂
则：n₁=

sini

sinr1

，n₂=

sini

sinr2

由几何知识得，红光和紫光在下表面出射点之间的距离为：
△x=dtanr₁-dtanr₂=d（

sinr1

cosr1

-

sinr2

cosr2

）=dsini（

1

n 2 1 -sin2i

-

1

n 2 2 -sin2i

）
答：①红光在玻璃中传播的速度为

c

n1

．
②红光和紫光在下表面出射点之间的距离为dsini（

1

n 2 1 -sin2i

-

1

n 2 2 -sin2i

）．

点评：本题的解题是运用几何知识分析红光和紫光在下表面出射点之间的距离与玻璃板厚度的关系，作出光路图是解答的基础．