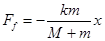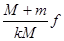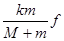题目内容
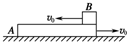 如图在光滑水平面上叠放AB两物体,其间有摩擦,mA=2kg,mB=1kg,速度的大小均为v0=10m/s,设A板足够长,当观察到B做加速运动时,A的可能速度为( )
如图在光滑水平面上叠放AB两物体,其间有摩擦,mA=2kg,mB=1kg,速度的大小均为v0=10m/s,设A板足够长,当观察到B做加速运动时,A的可能速度为( )分析:根据系统的动量守恒,求出物块与薄板相对静止时的共同速度,速度相同之后物块做加速运动.
解答:解:因摩擦力作用,A、B先必做减速运动,因初动量总和为mAv0-mBv0=2×10-1×10kg?m/s=10 kg?m/s,
故必是B先减速为零,后反向加速,最后与A一起向右运动.
整个过程中,A一直减速.当B速度为零时,A速度为v1,由动量守恒定律mAv0-mBv0=mAv1+0,
代人数据解得:v1=
m/s=5m/s,
AB最终速度为v2,则mAv0-mBv0=(mA+mB)v2
代人数据解得:v2=
m/s.可见,B做加速运动时,A的速度范围是5 m/s>vA>3.3 m/s.C正确.
故选:C
故必是B先减速为零,后反向加速,最后与A一起向右运动.
整个过程中,A一直减速.当B速度为零时,A速度为v1,由动量守恒定律mAv0-mBv0=mAv1+0,
代人数据解得:v1=
| 10 |
| 2 |
AB最终速度为v2,则mAv0-mBv0=(mA+mB)v2
代人数据解得:v2=
| 10 |
| 3 |
故选:C
点评:题运用动量守恒定律分析物体的运动状态,也可以运用牛顿第二定律和运动学公式分析.

练习册系列答案
相关题目
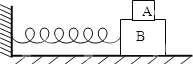
如图,两长方体木块A和B叠入在光滑水平面上,质量分别为m和M,A与B之间的最大静摩擦力为f,B与劲度系数为k的水平轻质弹簧连接构成弹簧振子。为使A和B 在振动过程中不发生相对滑动,则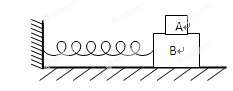
| A.它们的最大加速度不能大于f/m |
| B.它们的最大加速度不能大于f/M |
C.它们的振幅不能大于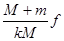 |
D.它们的振幅不能大于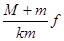 |
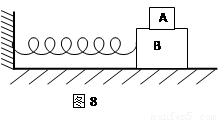
如图8所示,两长方体木块A和B叠入在光滑水平面上,质量分别为m和M,A与B之间的最大静摩擦力为f,B与劲度系数为k的水平轻质弹簧连接构成弹簧振子。A和B 在振动过程中始终不发生相对滑动,则( )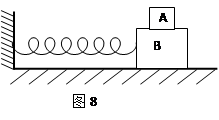
A.A受到B的摩擦力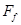 与B离开平衡位置位移x总满足 与B离开平衡位置位移x总满足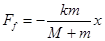 |
| B.它们的最大加速度不能大于f/M |
C.它们的振幅不可能大于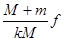 |
D.它们的振幅不可能大于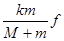 |



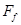 与B离开平衡位置位移x总满足
与B离开平衡位置位移x总满足