��Ŀ����
����Ŀ��(18��)��ͼ��ʾ��ˮƽ�����Ϲ̶�һľ�壬С����A����Ϊm��������Ϊ+q����ľ��֮��û��Ħ������С����B����Ϊ3m�������磬��ľ��֮���Ħ��������=0.5��ľ����߽�MN��PQ֮��ľ���Ϊl����������ǿ�糡���糡ǿ��E����qE=mg��B��ֹ�ڱ߽�PQ������A��ľ����˾�ֹ�ͷţ��˺�A��B�ᷢ����ײ��ÿ����ײ��Ϊ������ײ������ײǰ��A��B�ĵ������ֲ��䣬A��B������Ϊ�ʵ㣬�������ٶ�Ϊg��
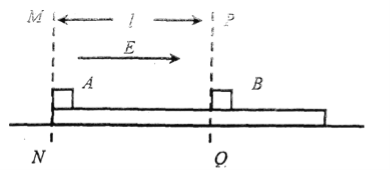
(1)���һ����ײ����ʱA��B���Ե��ٶȣ�
(2)��ľ���㹻������A�ڵ糡���˶�����ʱ�䣺
(3)��ľ���ܳ���Ϊ![]() ����A��B������ײ�Ĵ�����
����A��B������ײ�Ĵ�����
���𰸡���1��![]() ����������
����������![]() ���������ң���2��
���������ң���2��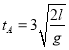 ��
��
��3��A��B������ײ3�Σ�
��������
�����������1������A��һ�θ��뿪�糡ʱ�ٶ�Ϊv0���ɶ��ܶ����ã�![]() ����qE=mg
����qE=mg
�� ![]()
A��B����������ײ��ȡ����Ϊ�������ɶ����غ��У�mv0=mvA1+3mvB1��
�������غ��:![]()
�ɵ�:![]() ����������
����������![]() ����������
����������
��2��Ȼ��B���Ҽ�����0�������˶��ļ��ٶ�Ϊa=��g����ʱ![]() ;
;
A�������ȼ����ٷ����ȼ��٣��ڵ糡ʱ��Ϊ![]() ����������B;������һ�ε�����ײ��������������֪��B�����˶���ʱ��������A�ڵ糡���˶���ʱ����ȣ���ÿ�ζ���A�Ͼ�ֹ��B����������ײ������ײ��֪��ÿ����ײ��A���ٶȴ�С���㣺
����������B;������һ�ε�����ײ��������������֪��B�����˶���ʱ��������A�ڵ糡���˶���ʱ����ȣ���ÿ�ζ���A�Ͼ�ֹ��B����������ײ������ײ��֪��ÿ����ײ��A���ٶȴ�С���㣺![]() ,��,
,��,![]()
�ڵ糡�е�ʱ��Ҳ��: ![]() ,����
,����![]()
���ڵ糡����������ٷ�����ٵ���ʱ��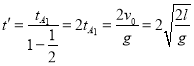
��һ�δӵ糡��˵��Ҷ˵�ʱ��Ϊ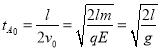
��A�ڵ糡���˶�����ʱ��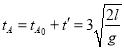
��3����һ����ײ��B�����ȼ��ٵ�λ��Ϊ![]()
����ÿ����ײ��B���ٶ�Ϊ��ײǰA���ٶȵ�һ�룬Ҳ��Ϊǰһ��B�Լ��ٶȵ�һ�룬���ÿ�������ȼ��ٵ�λ��Ϊǰһ�ε�![]() ����
����![]()
���A��B�ܷ���n����ײ����B���Ҳ��˶�����λ��Ϊ![]() Ӧ���㣺
Ӧ���㣺
![]() ��
��
�ɴ˿ɵ�:n=3
���ߣ�![]() ��
��![]() ��
��![]()
![]() ��
��![]()
�ɴ˿ɵ���������B��û�е���ȥ������������λ�ƴ���![]() ���Ѿ�����ȥ�ˣ�����3�Σ�
���Ѿ�����ȥ�ˣ�����3�Σ�

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�