题目内容
2.有两个大小相等的共点力,当它们的夹角为90°时合力F=10N,F1=5$\sqrt{2}$N,F25$\sqrt{2}$N;当它们的夹角为120°时合力F′=5$\sqrt{2}$N.分析 两个大小相等的共点力F1、F2,当它们间夹角为90°时合力大小为20N,根据平行四边形定则求出分力的大小,当夹角为120°时,再根据平行四边形定则求出合力的大小.
解答 解:两个大小相等的共点力为:F1=F2,
当两个力之间的夹角为90°时合力大小,根据平行四边形定则,知:
F=$\sqrt{{F}_{1}^{2}+{F}_{2}^{2}}$=10N;
解得:F1=F2=5$\sqrt{2}$N
当两个力夹角为120°时,根据平行四边形定则知合力为:
F′=5$\sqrt{2}$N.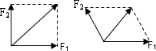
故答案为:5$\sqrt{2}$N,5$\sqrt{2}$N,5$\sqrt{2}$N.
点评 解决本题关键知道力的合成与分解遵循平行四边形定则,会根据平行四边形定则去求合力或分力.

练习册系列答案
相关题目
13.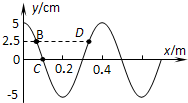 如图所示为一列简谐横波在t=0时刻的图象.此时质点C的运动方向沿y轴负方向,且当t=0.55s时质点C恰好第3次(从t=0时刻算起)到达y轴正方向最大位移处.下列选项中正确的是( )
如图所示为一列简谐横波在t=0时刻的图象.此时质点C的运动方向沿y轴负方向,且当t=0.55s时质点C恰好第3次(从t=0时刻算起)到达y轴正方向最大位移处.下列选项中正确的是( )
 如图所示为一列简谐横波在t=0时刻的图象.此时质点C的运动方向沿y轴负方向,且当t=0.55s时质点C恰好第3次(从t=0时刻算起)到达y轴正方向最大位移处.下列选项中正确的是( )
如图所示为一列简谐横波在t=0时刻的图象.此时质点C的运动方向沿y轴负方向,且当t=0.55s时质点C恰好第3次(从t=0时刻算起)到达y轴正方向最大位移处.下列选项中正确的是( )| A. | t=0时刻质点B与质点C速度方向相反,所以两质点为反相点 | |
| B. | 此波沿x轴负向传播,波速v=2m/s | |
| C. | 此波沿x轴正向传播,波速v=2m/s | |
| D. | 从t=0至t=1.2s的时间内,质点D运动的路程120 cm |
10. 如图所示,分别为一列横流在某一时刻的图象和在x=6cm处质点从该时刻开始计时的振动图象,这列波( )
如图所示,分别为一列横流在某一时刻的图象和在x=6cm处质点从该时刻开始计时的振动图象,这列波( )
 如图所示,分别为一列横流在某一时刻的图象和在x=6cm处质点从该时刻开始计时的振动图象,这列波( )
如图所示,分别为一列横流在某一时刻的图象和在x=6cm处质点从该时刻开始计时的振动图象,这列波( )| A. | 沿x轴的正向传播 | |
| B. | 波速为100cm/s | |
| C. | 该时刻以后,x=2.3cm处的质点比x=5m处的质点先回到平衡位置 | |
| D. | 该时刻起,x=2.5cm处的质点第一次回到平衡位置的时间t=0.035s |
17.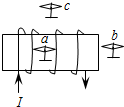 通有方向如图所示电流I的螺线管内外空间中,放有a、b、c三个小磁针,当三个小磁针静止时( )
通有方向如图所示电流I的螺线管内外空间中,放有a、b、c三个小磁针,当三个小磁针静止时( )
 通有方向如图所示电流I的螺线管内外空间中,放有a、b、c三个小磁针,当三个小磁针静止时( )
通有方向如图所示电流I的螺线管内外空间中,放有a、b、c三个小磁针,当三个小磁针静止时( )| A. | a、b、c右端都为S极 | B. | a、c右端都为S极,b左端为N极 | ||
| C. | a、b左端都为S极,c右端为N极 | D. | a、b左端都为N极,c左端为S极 |
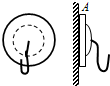 全国著名发明家邹德进发明了一种“吸盘式”挂衣钩,如图所示.将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品.如果挂衣钩的吸盘压紧时,它的圆面直径为$\frac{1}{{10\sqrt{π}}}$m,吸盘圆面压在墙上有$\frac{4}{5}$的面积跟墙面完全接触,中间$\frac{1}{5}$未接触部分间无空气.已知吸盘面与墙面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(取最大静摩擦力等于滑动摩擦力,大气压强p0=1.0×105Pa.)
全国著名发明家邹德进发明了一种“吸盘式”挂衣钩,如图所示.将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品.如果挂衣钩的吸盘压紧时,它的圆面直径为$\frac{1}{{10\sqrt{π}}}$m,吸盘圆面压在墙上有$\frac{4}{5}$的面积跟墙面完全接触,中间$\frac{1}{5}$未接触部分间无空气.已知吸盘面与墙面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(取最大静摩擦力等于滑动摩擦力,大气压强p0=1.0×105Pa.) 如图所示,有一条沿顺时针方向匀速传送的传送带,恒定速度v=4m/s,传送带与水平面的夹角θ=37°,现将质量m=1kg的小物块轻放在其底端(小物块可视作质点),与此同时,给小物块沿传送带方向向上的恒力F=6N,经过一段时间,小物块上到了离地面高为h=3m的平台上.已知物块与传送带之间的动摩擦因数μ=0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8).问:
如图所示,有一条沿顺时针方向匀速传送的传送带,恒定速度v=4m/s,传送带与水平面的夹角θ=37°,现将质量m=1kg的小物块轻放在其底端(小物块可视作质点),与此同时,给小物块沿传送带方向向上的恒力F=6N,经过一段时间,小物块上到了离地面高为h=3m的平台上.已知物块与传送带之间的动摩擦因数μ=0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8).问: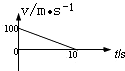 如图所示为一物体运动的v-t图线,则0-10s物体运动的加速度大小为10m/s2,10s内物体的位移为500m.
如图所示为一物体运动的v-t图线,则0-10s物体运动的加速度大小为10m/s2,10s内物体的位移为500m.