题目内容
(2010?肇庆一模)现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前,乙车在后,它们行驶的速度均为10m/s.当两车快要到一十字路口时,甲车司机看到绿灯已转换成了黄灯,于是紧急刹车(反应时间忽略不计),乙车司机为了避免与甲车相撞也紧急刹车,但乙车司机反应较慢(反应时间为0.5s).已知甲车紧急刹车时制动力为车重的0.4倍,乙车紧急刹车时制动力为车重的0.5倍,g取10m/s2.
(1)若甲车司机看到黄灯时车头距警戒线15m,他采取上述措施能否避免闯警戒线?
(2)为保证两车在紧急刹车过程中不相撞,甲、乙两车行驶过程中至少应保持多大距离?
(1)若甲车司机看到黄灯时车头距警戒线15m,他采取上述措施能否避免闯警戒线?
(2)为保证两车在紧急刹车过程中不相撞,甲、乙两车行驶过程中至少应保持多大距离?
分析:(1)甲刹车时,水平方向受到制动力,根据牛顿第二定律求出甲刹车时的加速度.由运动学速度-位移关系式求出速度减小到零时的位移大小,与15m比较,确定甲车能否避免闯警戒线.
(2)由乙车制动力,根据牛顿第二定律求出乙刹车时的加速度.当两车恰好相撞时的条件:速度相等,根据速度公式求出所用时间,应用位移公式求出两车的位移,再求解两车行驶过程中至少应保持的距离.
(2)由乙车制动力,根据牛顿第二定律求出乙刹车时的加速度.当两车恰好相撞时的条件:速度相等,根据速度公式求出所用时间,应用位移公式求出两车的位移,再求解两车行驶过程中至少应保持的距离.
解答:解:
(1)根据牛顿第二定律可得:甲车紧急刹车的加速度a1=
=
=4m/s2
这段时间滑行距s=
将数据代入解得:s=12.5m
因为s<15m,所以甲车司机能避免闯警戒线.
(2)设甲、乙两车行驶过程中至少应保持距s0,在乙车刹车t2时间两车恰好相撞,则有:
乙车紧急刹车的加速度为a2=
=
=5m/s2
v0-a1(t2+t0)=v0-a2t2
代入解得t2=2s
乙车通过的位移大小 s乙=v0t0+v0t2-
a2t22=15m
甲车通过的位移大小 s甲=v0(t0+t2)-
a1(t0+t2)2=12.5m.
代入解得 s0=s乙-s甲=(15-12.5)m=2.5m
答:(1)若甲车司机看到黄灯时车头距警戒线15m,他采取上述措施能避免闯警戒线.
(2)为保证两车在紧急刹车过程中不相撞,甲、乙两车行驶过程中至少应保持2.5m距离.
(1)根据牛顿第二定律可得:甲车紧急刹车的加速度a1=
| f1 |
| m1 |
| 0.4m1g |
| m1 |
这段时间滑行距s=
| ||
| 2a1 |
将数据代入解得:s=12.5m
因为s<15m,所以甲车司机能避免闯警戒线.
(2)设甲、乙两车行驶过程中至少应保持距s0,在乙车刹车t2时间两车恰好相撞,则有:
乙车紧急刹车的加速度为a2=
| f2 |
| m2 |
| 0.5m2g |
| m2 |
v0-a1(t2+t0)=v0-a2t2
代入解得t2=2s
乙车通过的位移大小 s乙=v0t0+v0t2-
| 1 |
| 2 |
甲车通过的位移大小 s甲=v0(t0+t2)-
| 1 |
| 2 |
代入解得 s0=s乙-s甲=(15-12.5)m=2.5m
答:(1)若甲车司机看到黄灯时车头距警戒线15m,他采取上述措施能避免闯警戒线.
(2)为保证两车在紧急刹车过程中不相撞,甲、乙两车行驶过程中至少应保持2.5m距离.
点评:本题第(1)问也可以用动能定理求解:-f1s=0-
m
,s=12.5m.第(2)问关键是抓住恰好相撞的条件:两车速度相同.
| 1 |
| 2 |
| v | 2 0 |

练习册系列答案
相关题目
 (2010?肇庆一模)如图所示,理想变压器的输入端接正弦交流电,副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开.当K接通时,以下说法中正确的是( )
(2010?肇庆一模)如图所示,理想变压器的输入端接正弦交流电,副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开.当K接通时,以下说法中正确的是( )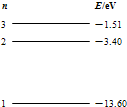 (2010?肇庆一模)使某种金属X发生光电效应所需的光子最小的能量为2.60eV.已知一群氢原子处于量子数n=3的激发态,其能级如右图所示.这些氢原子能够自发地跃迁到较低的能量状态,并向外辐射多种频率的光.那么,若用这些氢原子辐射的光照射这种金属,能够使这种金属X发生光电效应的有几种不同频率的光( )
(2010?肇庆一模)使某种金属X发生光电效应所需的光子最小的能量为2.60eV.已知一群氢原子处于量子数n=3的激发态,其能级如右图所示.这些氢原子能够自发地跃迁到较低的能量状态,并向外辐射多种频率的光.那么,若用这些氢原子辐射的光照射这种金属,能够使这种金属X发生光电效应的有几种不同频率的光( )