题目内容
【题目】如图所示,装置A由1/4圆弧CD部分(光滑)和水平DE部分(粗糙)组成,总质量为M = 0.6 kg,O为圆弧的圆心,其半径为R = 0.3 m,装置放在光滑水平面上,但是被锁定(锁定装置图中未画出)。质量为m = 0.3 kg的小物块B,从与O点在同一水平面上的C点由静止放开,物块B在水平部分DE上滑行时,与接触面间的动摩擦因数为μ= 0.1,重力加速度g取10 m/s2。试分析:
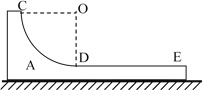
(1)物块B到达圆弧最低点D时对圆弧的压力大小;
(2)若将装置A的锁定解除,使其可以自由移动。则物块B从开始下滑到与A相对静止的过程中,物块B在水平DE部分相对于D点的最大距离为多少?该过程中装置A对地的位移为多少?
【答案】(1)![]() (2)
(2) ![]() ,
, ![]()
【解析】试题分析(1)从C到D由机械能守恒求出在C点的速度,由牛顿第二定律求出在D点的支持力,由牛顿第三定律求出对轨道的压力;(2)由能量守恒求出最大距离;由动量守恒和两者位移关系求出A对地的位移。
(1)从C→D过程,由机械能守恒得: ![]()
在D点,由牛顿第二定律得: ![]()
联立解得:N=9N
由牛顿第三定律得: ![]()
(2)物块B从开始下滑到与A相对静止的过程中
由能量守恒定律得: ![]()
解得:x = 3m
物块B从开始下滑到与A相对静止的过程中,由动量守恒定律得: ![]()
又![]()
联立解得: ![]()
且![]()
解得: ![]()

练习册系列答案
相关题目