题目内容
5.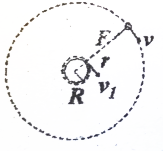 已知地球半径R,地球表面重力加速度g.卫星m绕地球做圆周运动,轨道半径为r.求:
已知地球半径R,地球表面重力加速度g.卫星m绕地球做圆周运动,轨道半径为r.求:(1)卫星的加速度a;
(2)卫星的线速度v;
(3)卫星的角速度ω;
(4)卫星的周期T;
(5)卫星的动能n.
分析 由万有引力提供向心力:G$\frac{Mm}{{r}^{2}}$=ma=m$\frac{{v}^{2}}{r}$=mrω2=mr$\frac{4{π}^{2}}{{T}^{2}}$ 从而可求得各量的表达式.
解答 解:由G$\frac{Mm}{{r}^{2}}$=ma=m$\frac{{v}^{2}}{r}$=mrω2=mr$\frac{4{π}^{2}}{{T}^{2}}$ ①
又GM=gR2 ②
联立以上2式可得:
(1)由G$\frac{Mm}{{r}^{2}}$=ma 与GM=gR2:可得a=$\frac{g{R}^{2}}{{r}^{2}}$
(2)由G$\frac{Mm}{{r}^{2}}$a=m$\frac{{v}^{2}}{r}$ 与GM=gR2:可得 v=$\sqrt{\frac{g{R}^{2}}{r}}$
(3)由G$\frac{Mm}{{r}^{2}}$=ma=m$\frac{{v}^{2}}{r}$=mrω2 与GM=gR2 得ω=$\sqrt{\frac{g{R}^{2}}{{r}^{3}}}$
(4)G$\frac{Mm}{{r}^{2}}$=mr$\frac{4{π}^{2}}{{T}^{2}}$ 又GM=gR2 得 T=$2π\sqrt{\frac{{r}^{3}}{GM}}$
(5)n=$\frac{1}{2}m\frac{g{R}^{2}}{r}$
答:(1)卫星的加速度a为=$\frac{g{R}^{2}}{{r}^{2}}$
(2)卫星的线速度为$\sqrt{\frac{g{R}^{2}}{r}}$
(3)卫星的角速度为$\sqrt{\frac{g{R}^{2}}{{r}^{3}}}$
(4)卫星的周期T为T=$2π\sqrt{\frac{{r}^{3}}{GM}}$;
(5)卫星的动能为$\frac{1}{2}m\frac{g{R}^{2}}{r}$n
点评 关键知道万有引力提供向心力,明确黄金定律是解题的关键.

| A. | 该卫星可能是同步卫星 | |
| B. | 地球自转周期一定是该卫星运行周期的整数倍 | |
| C. | 该卫星平面一定与东经115°52′所确定的平面共面 | |
| D. | 该卫星平面可能与南纬31°52′所确定的平面共面 |
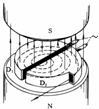
| A. | 图中加速器出口射出的是带正电粒子 | |
| B. | D形盒的狭缝间所加的电压是直流电压 | |
| C. | 强磁场对带电粒子做功,使其动能增大 | |
| D. | 粒子在加速器中的半径越大,周期越长 |
| A. | 温度传感器 | B. | 红外传感器 | C. | 声音传感器 | D. | 湿度传感器 |
 在购物的商场里我们常见到如图的电梯,图甲为阶梯电梯,图乙为斜面电梯,设两电梯的乘客随电梯匀速上行,则乘客受到电梯的( )
在购物的商场里我们常见到如图的电梯,图甲为阶梯电梯,图乙为斜面电梯,设两电梯的乘客随电梯匀速上行,则乘客受到电梯的( )| A. | 摩擦力的方向都相同 | B. | 支持力的大小都相同 | ||
| C. | 支持力的方向都相同 | D. | 作用力的大小与方向均相同 |
 如图所示,足够长的平行光滑金属导轨竖直放置,轨道间距为l,其上端接一阻值恒为R的灯泡L.在水平虚线L1、L2间有垂直导轨平面的匀强磁场,磁场区域的宽度为d,导体棒a的质量为2m、电阻为R;导体棒b的质量为m、电阻为2R,与导轨始终保持良好接触,它们分别从图中M、N处同时由静止开始沿导轨下滑,且都能匀速穿过磁场区域,当b刚穿过磁场时a正好进入磁场.设重力加速度为g,不计a、b棒之间的相互作用,导体棒始终与导轨垂直.求:
如图所示,足够长的平行光滑金属导轨竖直放置,轨道间距为l,其上端接一阻值恒为R的灯泡L.在水平虚线L1、L2间有垂直导轨平面的匀强磁场,磁场区域的宽度为d,导体棒a的质量为2m、电阻为R;导体棒b的质量为m、电阻为2R,与导轨始终保持良好接触,它们分别从图中M、N处同时由静止开始沿导轨下滑,且都能匀速穿过磁场区域,当b刚穿过磁场时a正好进入磁场.设重力加速度为g,不计a、b棒之间的相互作用,导体棒始终与导轨垂直.求:
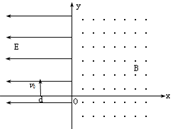 如图,在x<0的空间中,存在沿x轴负方向的匀强电场,电场强度E=10N/C;在x>0的空间中,存在垂直xy平面方向向外的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在距O点左边x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求
如图,在x<0的空间中,存在沿x轴负方向的匀强电场,电场强度E=10N/C;在x>0的空间中,存在垂直xy平面方向向外的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在距O点左边x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求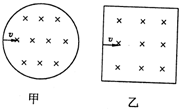 如图甲、乙是场强相同的圆形、正方形匀强磁场区域(圆形直径与正方形边长相同).不计重力的相同带电粒子以相同速度沿垂直于磁场方向飞入两个磁场区域,进入圆形磁场的粒子初速度方向对准圆心,进入正方形磁场的粒子初速度方向垂直于边界且从中点进入,则粒子分别经过两个磁场区域后,其速度变化△v甲、△v乙的大小关系为( )
如图甲、乙是场强相同的圆形、正方形匀强磁场区域(圆形直径与正方形边长相同).不计重力的相同带电粒子以相同速度沿垂直于磁场方向飞入两个磁场区域,进入圆形磁场的粒子初速度方向对准圆心,进入正方形磁场的粒子初速度方向垂直于边界且从中点进入,则粒子分别经过两个磁场区域后,其速度变化△v甲、△v乙的大小关系为( )