题目内容
2.A、B两物体的运动都发生在同一直线上,A某时刻的速度为2m/s,以0.2m/s2的加速度做匀减速前进,2s后与原来静止的B发生碰撞,碰撞后A以碰撞前的速率的一半反向弹回,仍做匀减速运动,加速度的值不变; B获得0.6m/s的速度,以0.4m/s2的加速度做匀减速运动.不计碰撞所用的时间.求:(1)碰后B运动的总时间;
(2)碰后A、B之间的最远距离.
分析 (1)B获得速度后做匀减速运动,已知初速度、加速度和末速度,由速度时间公式求解B运动的总时间.
(2)由匀变速运动的速度公式求出两球发生碰撞前瞬间A的速度,求出碰后A的速度,然后由匀变速运动的位移公式求出A、B静止时的位移,然后求出A、B间的最远距离.
解答 解:(1)对于B的匀减速运动,已知v0B=0.6m/s,aB=-0.4m/s2,vB=0
则碰后B运动的总时间为 tB=$\frac{{v}_{B}-{v}_{0B}}{{a}_{B}}$=$\frac{0-0.6}{-0.4}$=1.5s
(2)两球碰撞前瞬时,A的速度 vA=v0-aAt=2-0.2×2=1.6m/s,
碰后A的速度 vA′=$\frac{{v}_{A}}{2}$=0.8m/s,方向与原方向相反
碰后A、B做匀减速运动,由匀变速运动的速度位移公式 v2-v02=2ax,
可得碰后B运动的总位移:xB=$\frac{0-{v}_{0B}^{2}}{2{a}_{B}}$=$\frac{-0.{6}^{2}}{2×(-0.4)}$m=0.45m
A运动的总位移为 xA=$\frac{0-{v}_{A}^{′2}}{2(-{a}_{A})}$=$\frac{-0.{8}^{2}}{2×(-0.2)}$=0.8m
故碰后A、B之间的最远距离 s=xA+xB=0.8+0.45=1.25m;
答:
(1)碰后B运动的总时间是1.5s;
(2)碰后A、B之间的最远距离是1.25m.
点评 解决本题的关键理清A、B的运动情况,结合匀变速运动的运动学公式,灵活解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设地球表面重力加速度为g,物体在距地心4R(R为地球半径)处,由于地球的作用而产生的加速度为g′,则g:g′为( )
| A. | 1:1 | B. | 9:1 | C. | 4:1 | D. | 16:1 |
17.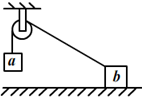 如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )
如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )
 如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )
如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )| A. | a的动能小于b的动能 | |
| B. | 两物体机械能的变化量相等 | |
| C. | a的重力势能的减小量大于两物体总动能的增加量 | |
| D. | 绳的拉力对a所做的功与对b所做的功的代数和为零 |
7. 如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )
如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )
 如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )
如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )| A. | E1>E2、r1>r2 | B. | E1=E2、r1>r2 | C. | E1>E2、r1=r2 | D. | E1>E2、r1<r2 |
14.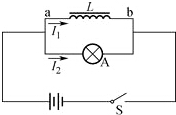 如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )
如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )
 如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )
如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )| A. | 线圈L中的电流I1立即减为零 | |
| B. | 线圈L的b端电势高于a端 | |
| C. | 小灯泡A中的电流由I1逐渐减为零,方向与I2相反 | |
| D. | 小灯泡A中的电流I2逐渐减为零,方向与原来相反 |
12.关于竖直上抛运动,下列说法中正确的是( )
| A. | 在最高点速度为零,加速度也为零 | |
| B. | 上升过程中速度向上,加速度向下 | |
| C. | 在最高点速度为零,物体处于平衡状态 | |
| D. | 上升到某一高度时的速度与下降到此高度时的速度大小相等 |
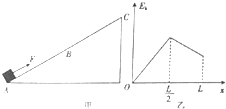 如图甲所示,将一块长度为$\frac{L}{2}$的表面光滑的金属板AB的另一块长度也为$\frac{L}{2}$的表面粗糙的木板BC平滑地拼接在一起组成斜面AC,并将一小物块在平行于斜面的恒定拉力F作用下由静止从A运动到C,历时为t0,小物块的动能Ek随位移x的变化情况如图乙所示,则小物块的速度v、加速度大小a、重力势能Ep随时间t(或位移x)变化情况的下列图中,可能正确的有( )
如图甲所示,将一块长度为$\frac{L}{2}$的表面光滑的金属板AB的另一块长度也为$\frac{L}{2}$的表面粗糙的木板BC平滑地拼接在一起组成斜面AC,并将一小物块在平行于斜面的恒定拉力F作用下由静止从A运动到C,历时为t0,小物块的动能Ek随位移x的变化情况如图乙所示,则小物块的速度v、加速度大小a、重力势能Ep随时间t(或位移x)变化情况的下列图中,可能正确的有( )


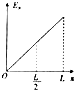
 某实验小组利用拉力传感器、光电门等器材探究滑块“动能定理”的实验,实验装置如图所示,在滑块上安装一遮光条与拉力传感器,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电门安装在B处.测得滑块(含遮光板和拉力传感器)质量为M、钩码总质量为m、AB之间的距离为L,当地的重力加速度为g.将滑块在如图A位置由静止释放后,拉力传感器记录下滑块在运动过程的拉力为F,光电计时器记录下遮光条通过光电门的时间分别为△t.
某实验小组利用拉力传感器、光电门等器材探究滑块“动能定理”的实验,实验装置如图所示,在滑块上安装一遮光条与拉力传感器,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电门安装在B处.测得滑块(含遮光板和拉力传感器)质量为M、钩码总质量为m、AB之间的距离为L,当地的重力加速度为g.将滑块在如图A位置由静止释放后,拉力传感器记录下滑块在运动过程的拉力为F,光电计时器记录下遮光条通过光电门的时间分别为△t.