题目内容
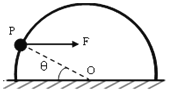
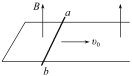
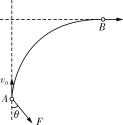
【题目】如图所示,在光滑水平桌面上有一个质量为m的质点,在沿平行于桌面方向的恒定外力F作用下,以初速度v0从A点开始做曲线运动,图中曲线是质点的运动轨迹。已知在t s末质点的速度达到最小值v,到达B点时的速度方向与初速度v0的方向垂直,则
A. 恒定外力F的方向与初速度的反方向成θ角指向曲线内侧,且![]()
B. 质点所受合外力的大小为![]()
C. 质点到达B点时的速度大小为![]()
D. t s内恒力F做功为![]()
【答案】ABC
【解析】
分析可知,恒力F的方向应与速度方向成钝角,如图所示:
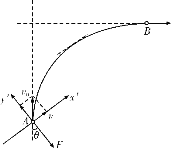
在x′方向上由运动学知识得 v=v0sin θ ;在y′方向上由运动学知识得v0cos θ=ayt;由牛顿第二定律有F=may ;解得F=![]() ,sin θ=
,sin θ=![]() ,即恒力F的方向与初速度的反方向成θ角指向曲线内侧,且sin θ=
,即恒力F的方向与初速度的反方向成θ角指向曲线内侧,且sin θ=![]() 。故AB正确;设质点从A点运动到B历时t1,设在v0方向上的加速度大小为a1,在垂直v0方向上的加速度大小为a2,由牛顿第二定律有Fcos θ=ma1;Fsin θ=ma2;由运动学知识可得v0=a1t1;vB=a2t1解得vB=
。故AB正确;设质点从A点运动到B历时t1,设在v0方向上的加速度大小为a1,在垂直v0方向上的加速度大小为a2,由牛顿第二定律有Fcos θ=ma1;Fsin θ=ma2;由运动学知识可得v0=a1t1;vB=a2t1解得vB=![]() ,则选项C正确;t s内恒力F做功为-
,则选项C正确;t s内恒力F做功为-![]() m(v02-v2) ,故D错误。故选ABC.
m(v02-v2) ,故D错误。故选ABC.

练习册系列答案
相关题目