题目内容
（2007?佛山一模）物体A放在水平面上与半径为r的圆柱体B用跨过定滑轮的细线相连接，半径为R的圆柱体C穿过细绳后搁在B上，三个物体的质量分别为mA=0.8kg，mB=mC=0.1kg．现让它们由静止开始运动，B下降h1=0.5m后，C被内有圆孔（半径为R′）的支架D挡住（r＜R′＜R），而B穿过圆孔继续下降，当B再下降h2=0.3m时才停止下落，运动的初末状态分别如图甲、乙所示．试求物体A与水平面间的动摩擦因数．滑轮的摩擦、细线和C之间的摩擦以及空气阻力均不计，g取10m/s2．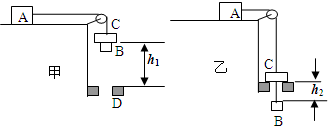
分析：A先做匀加速直线运动，后做匀减速直线运动，根据速度-位移关系公式分别研究这两个过程，得到加速度之比．根据牛顿第二定律分别研究加速和减速运动过程，采用隔离法，得到加速度的表达式，再求解动摩擦因数μ．
解答：解：设加速运动的末速度为v，由运动学公式得：
匀加速过程：v2=2a1H1 ①
匀减速过程：v2=2a2H2 ②
由①：②得：a1：a2=3：5
设A、B、C一起下降时绳中拉力为F1，C被固定挡板D截住，B继续下降时绳中拉力为F2
根据牛顿第二定律，有
匀加速过程：
对A：F1-μmAg=mAa1 ③
对BC整体：（mB+mC）g-F1=（mB+mC）a1 ④
由③④联立得：a1=
⑤
匀减速过程：
对A：μmAg-F2=mAa2 ⑥
对B：F2-mBg=mBa2 ⑦
联立⑥⑦得：a2=
⑧
联立⑤⑧两式，解得：μ=0.2
答：物体A与平面的动摩擦因数μ=0.2．
匀加速过程：v2=2a1H1 ①
匀减速过程：v2=2a2H2 ②
由①：②得：a1：a2=3：5
设A、B、C一起下降时绳中拉力为F1，C被固定挡板D截住，B继续下降时绳中拉力为F2
根据牛顿第二定律，有
匀加速过程：
对A：F1-μmAg=mAa1 ③
对BC整体：（mB+mC）g-F1=（mB+mC）a1 ④
由③④联立得：a1=
| (mB+mc)g-μmAg |
| mA+mB+mC |
匀减速过程：
对A：μmAg-F2=mAa2 ⑥
对B：F2-mBg=mBa2 ⑦
联立⑥⑦得：a2=
| μmAg-mBg |
| mA+mB |
联立⑤⑧两式，解得：μ=0.2
答：物体A与平面的动摩擦因数μ=0.2．
点评：本题是连接体问题，由于A与B加速度大小相等，方向不同，一般采用隔离法研究加速度．本题也可以运用动能定理处理．
练习册系列答案
相关题目
（2007?佛山一模）如图将一个小球以速度v0从O点水平抛出，使小球恰好能够垂直打在斜面上．若斜面的倾角为α，重力加速度为g，小球从抛出到打到斜面在空中飞行的时间为t，那么下述说法中不正确的是（ ）
（2007?佛山一模）如图所示，猎人非法猎猴，用两根轻绳将猴子悬于空中，猴子处于静止状态．以下相关说法正确的是（ ）
（2007?佛山一模）小球从空中自由下落，与水平地面相碰后弹到空中某一高度，其速度随时间变化的关系如图所示，则（ ）
（2007?佛山一模）如图所示，在光滑绝缘水平面上的M、N两点各放有一个电荷量分别为+q和+2q的完全相同的金属球A、B．在某时刻，使A、B以相等的初动能E开始沿同一直线相向运动（这时它们的动量大小为P），若它们在碰撞过程中无机械能损失，碰后又各自返回．它们返回M、N两点时的动能分别为E1和E2，动量大小分别为P1和P2，则下列结论正确的是（ ）