题目内容
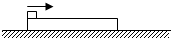
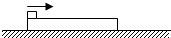
 如图,一质量为M的长木板静止在水平面上,有一质量为m的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为μ0,最大静摩擦力等于滑动摩
如图,一质量为M的长木板静止在水平面上,有一质量为m的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为μ0,最大静摩擦力等于滑动摩擦力,求:
(1)若滑块在木板上滑动时,木板能保持静止不动,木板和地面之间的动摩擦因数须满足什么条件?
(2)若长木板的质量M=0.2kg,长木板与水平面间的动摩擦因数μ=0.1.滑块的质量也为0.2kg.滑块以v0=1.2m/s的速度滑上长木板的左端,小滑块与长木板间的动摩擦因数μ0=0.4.滑块最终没有滑离长木板,求滑块在开始滑上长木板到最后静止下来的过程中,滑块滑行的距离是多少?(g=10m/s2)
分析:(1)长木板受到滑块向前的摩擦力f1,还受到地面给它的摩擦力,当f1≤fmax时木板能保持静止不动,根据题意即可求解;
(2)小滑块在滑动摩擦力作用下,做匀减速运动,木板在摩擦力作用下做匀加速运动,当速度相等时相对静止,然后一起做匀减速运动直到静止,先求出速度相等前运动的位移,速度相同后一起做匀减速运动,求出加速度,根据运动学公式即可求解.
(2)小滑块在滑动摩擦力作用下,做匀减速运动,木板在摩擦力作用下做匀加速运动,当速度相等时相对静止,然后一起做匀减速运动直到静止,先求出速度相等前运动的位移,速度相同后一起做匀减速运动,求出加速度,根据运动学公式即可求解.
解答:解:(1)长木板受到滑块向前的摩擦力f1=μ0mg
设长木板与地面之间的动摩擦因数为μ
长木板受到地面的最大静摩擦力大小fmax=μ(M+m)g
由题意得:当f1≤fmax时木板能保持静止不动,
即:μ≥
μ0
(2)对m:μ2mg=ma2 解得:a2=4m/s2
对M:μ2mg-μ1(M+m)g=Ma1 解得:a1=2m/s2
设经历时间为t两者速度相同,则:v0-a2t=a1t
解得:t=0.2s
两者共同速度为:v=a1t=0.4m/s
两者相对静止前,小滑块的位移:s1=v0t-
a2t2=0.16m
达到共同速度后对滑块和木板:μ1(M+m)g=(M+m)a3
滑行位移为:s2=
解得:s2=0.08m
小滑块的总位称为:s=s1+s2=0.24m
答:(1)若滑块在木板上滑动时,木板能保持静止不动,木板和地面之间的动摩擦因数须满足μ≥
μ0;
(2)滑块滑行的距离是0.24m.
设长木板与地面之间的动摩擦因数为μ
长木板受到地面的最大静摩擦力大小fmax=μ(M+m)g
由题意得:当f1≤fmax时木板能保持静止不动,
即:μ≥
| m |
| M+m |
(2)对m:μ2mg=ma2 解得:a2=4m/s2
对M:μ2mg-μ1(M+m)g=Ma1 解得:a1=2m/s2
设经历时间为t两者速度相同,则:v0-a2t=a1t
解得:t=0.2s
两者共同速度为:v=a1t=0.4m/s
两者相对静止前,小滑块的位移:s1=v0t-
| 1 |
| 2 |
达到共同速度后对滑块和木板:μ1(M+m)g=(M+m)a3
滑行位移为:s2=
| v2 |
| 2a3 |
解得:s2=0.08m
小滑块的总位称为:s=s1+s2=0.24m
答:(1)若滑块在木板上滑动时,木板能保持静止不动,木板和地面之间的动摩擦因数须满足μ≥
| m |
| M+m |
(2)滑块滑行的距离是0.24m.
点评:解题的关键是正确对滑块和木板进行受力分析,清楚滑块和木板的运动情况,根据牛顿第二定律及运动学基本公式求解,难度适中.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图所示质量为M的长木板静止在光滑平面上,另一质量为m的木块以水平初速度v0从左端滑上长木板,经时间t从长木板的另一端滑下.若木块和长木板之间的动摩擦因数为μ,求木块滑下时长木板的速度.
如图所示质量为M的长木板静止在光滑平面上,另一质量为m的木块以水平初速度v0从左端滑上长木板,经时间t从长木板的另一端滑下.若木块和长木板之间的动摩擦因数为μ,求木块滑下时长木板的速度.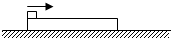 如图,一质量为M的长木板静止在水平面上,有一质量为m的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为μ0,最大静摩擦力等于滑动摩
如图,一质量为M的长木板静止在水平面上,有一质量为m的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为μ0,最大静摩擦力等于滑动摩