题目内容
(14分)如图所示,将直径为2R的半圆形导轨固定在竖直面内的A、B两点,直径AB与竖直方向的夹角为60°。在导轨上套一质量为m的小圆环,原长为2R、劲度系数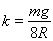 的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,且形变量为x时具有弹性势能
的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,且形变量为x时具有弹性势能 ,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求

(1)圆环的速率v;
(2)导轨对圆环的作用力F的大小?
【答案】
 ?? ?
?? ? 
【解析】

(1)由几何知识得,圆环在C点、D点时,弹性绳形变量相同,弹性势能相等。由机械能守恒定律,有
 ??????????????????????? 3分
??????????????????????? 3分
由几何关系可知  ???????????????????? 2分
???????????????????? 2分
解得  ???????????????????????????? 3分
???????????????????????????? 3分
(2)圆环在D点受力如图,弹性绳的弹力
 ??????????????????????????????????? 1分
??????????????????????????????????? 1分
其中 ????????????????????????? 1分
????????????????????????? 1分
由牛顿第二定律,有
 ?????? 2分
?????? 2分
解得 ?????????????????????????? 2分
?????????????????????????? 2分
考点:本题考查牛顿定律和功能关系。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图所示,将直径为d,电阻为R的闭合金属环从匀强磁场B拉出,求这一过程中
如图所示,将直径为d,电阻为R的闭合金属环从匀强磁场B拉出,求这一过程中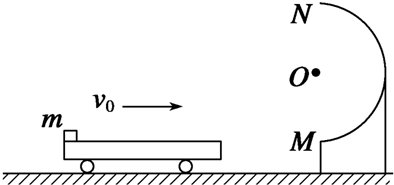
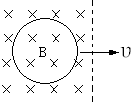
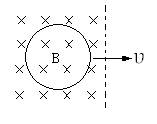 (10分)如图所示,将直径为
(10分)如图所示,将直径为