��Ŀ����
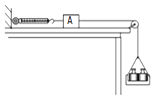
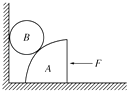
����Ŀ����ͼ��ʾ���ֲڵ�ˮƽ���Ͼ�ֹ��������������Ϊm��Сľ�䣬������Сľ��ľ����Ϊl �� ��������ˮƽ�������������ߵ�С����ʹ֮���һ�������һ������Сľ�䵯����ײ��ÿ�ε�����ײ��Сľ�䶼����һ���˶������������й��˵��������䣬���ǡ������������ľ�������˶�����֪Сľ����ˮƽ���Ķ�Ħ������Ϊ�� �� �������ٶ�Ϊg �� �赯����ײʱ�伫�̣�Сľ�����Ϊ�ʵ㣮��һ�ε�����ײ�͵ڶ��ε�����ײ��ľ����ʧ�Ļ�е��֮�ȣ�![]()
���𰸡�����������ľ�������˶�����ƽ�������ã�F=3��mg ��
ˮƽ��������ߵ�ľ��ʱ�����ݶ��ܶ����У���F����mg��l= ![]() mv12��0��
mv12��0��
ľ�䷢����һ�ε�����ײ��������Ϊ�������ݶ����غ㶨���У�mv1=2mv2 ��
������ײ����ʧ�Ļ�е��Ϊ����E1= ![]() mv12��
mv12�� ![]() 2mv22 ��
2mv22 ��
��һ������ˮƽ������ľ�������˶������ݶ��ܶ�����
��F��2��mg��l= ![]() 2mv32��
2mv32�� ![]() 2mv22 ��
2mv22 ��
ľ�䷢���ڶ��ε�����ײ��������Ϊ�������ݶ����غ㶨���У�2mv3=3mv4 ��
������ײ����ʧ�Ļ�е��Ϊ����E2= ![]() 2mv32��
2mv32�� ![]() 3mv42 ��
3mv42 ��
�������ľ�����ε�����ײ��������ʧ�Ļ�е��֮��Ϊ�� ![]() ��
��
�𣺵�һ�ε�����ײ�͵ڶ��ε�����ײ��ľ����ʧ�Ļ�е��֮��Ϊ3��2��
��������ľ�鵯����ײ����ϵͳ�����غ㣬Ӧ�ö��ܶ���������嵯����ײǰ���ٶȣ�Ӧ�ö����غ㶨���������غ㶨�����������ײ������ʧ�Ļ�е�ܣ�Ȼ�������ʧ�Ļ�е��֮�ȣ�
�����㾫����������Ҫ�����˶����غ㶨�ɵ����֪ʶ�㣬��Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��������ȷ�����⣮

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�