题目内容
(1)如图甲所示,某同学在做“研究匀变速直线运动”的实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T=0.10s,其中s1=5.12cm,s2=5.74cm,s3=6.14cm,s4=7.05cm,s5=7.68cm,s6=8.33cm、则打F点时小车的瞬时速度的大小是 m/s,加速度大小是 m/s2.(计算结果保留两位有效数字)(2)有人说矿区的重力加速度偏大,某同学“用单摆测定重力加速度”的实验探究该问题.他用最小分度为毫米的米尺测得摆线的长度为800.0mm,用游标为10分度的卡尺测得摆球的直径如图乙所示,摆球的直径为 mm.他把摆球从平衡位置拉开一个小角度由静止释放,使单摆在竖直平面内摆动,当摆动稳定后,在摆球通过平衡位置时启动秒表,并数下“0”,直到摆球第30次同向通过平衡位置时按停秒表,秒表读数如图丙所示,读出所经历的时间t,则单摆的周期为 s,该实验测得当地的重力加速度为 m/s2.(保留3位有效数字)

【答案】分析:(1)纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.
(2)10分度的游标卡尺每一分度表示的长度为0.1mm.由主尺读出整米数,由游标尺读出毫米的小数部分.
由秒表读出时间t,由T=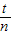 求出单摆的周期,再由单摆的周期公式求出重力加速度g.
求出单摆的周期,再由单摆的周期公式求出重力加速度g.
解答:解:(1)利用匀变速直线运动的推论得中间时刻速度等于这段过程中的平均速度,
所以vF=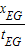 =
=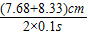 =0.80m/s,
=0.80m/s,
根据运动学公式采用逐差法求解加速度得:
a1=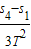
a2=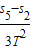
a3=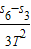
a=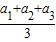 =
=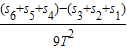 =0.64m/s2.
=0.64m/s2.
故答案为:0.80,0.64
(2)主尺读数为20mm.10分度的游标卡尺每一分度表示的长度为0.1mm,游标尺第2条刻度线与主尺对齐,则游标尺读数为0.2mm,摆球的直径为20mm+0.2mm=20.2mm.
由秒表读出单摆做300次全振动所用的时间t=54.0s,单摆的周期T=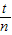 =1.80s.
=1.80s.
单摆的摆长l=摆线的长度+摆球的半径=800.0mm+10.1mm=810.1mm.
由单摆的周期公式T=2π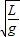 得,
得,
重力加速度g=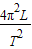 ,代入解得,g=9.86m/s2
,代入解得,g=9.86m/s2
故答案为:(1)0.80,0.64
(2)20.2,1.80,9.86.
点评:(1)要注意单位的换算和有效数字的保留.
对于相邻的计数点位移间隔不等时能够运用逐差法求解.
(2)单摆的摆长等于悬点到球心的距离,即等于摆线的长度与摆球的半径之和,不能漏掉球的半径.
(2)10分度的游标卡尺每一分度表示的长度为0.1mm.由主尺读出整米数,由游标尺读出毫米的小数部分.
由秒表读出时间t,由T=
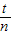 求出单摆的周期,再由单摆的周期公式求出重力加速度g.
求出单摆的周期,再由单摆的周期公式求出重力加速度g.解答:解:(1)利用匀变速直线运动的推论得中间时刻速度等于这段过程中的平均速度,
所以vF=
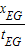 =
=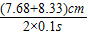 =0.80m/s,
=0.80m/s,根据运动学公式采用逐差法求解加速度得:
a1=
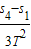
a2=
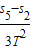
a3=
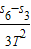
a=
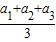 =
=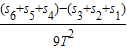 =0.64m/s2.
=0.64m/s2.故答案为:0.80,0.64
(2)主尺读数为20mm.10分度的游标卡尺每一分度表示的长度为0.1mm,游标尺第2条刻度线与主尺对齐,则游标尺读数为0.2mm,摆球的直径为20mm+0.2mm=20.2mm.
由秒表读出单摆做300次全振动所用的时间t=54.0s,单摆的周期T=
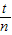 =1.80s.
=1.80s.单摆的摆长l=摆线的长度+摆球的半径=800.0mm+10.1mm=810.1mm.
由单摆的周期公式T=2π
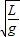 得,
得,重力加速度g=
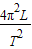 ,代入解得,g=9.86m/s2
,代入解得,g=9.86m/s2故答案为:(1)0.80,0.64
(2)20.2,1.80,9.86.
点评:(1)要注意单位的换算和有效数字的保留.
对于相邻的计数点位移间隔不等时能够运用逐差法求解.
(2)单摆的摆长等于悬点到球心的距离,即等于摆线的长度与摆球的半径之和,不能漏掉球的半径.

练习册系列答案
相关题目
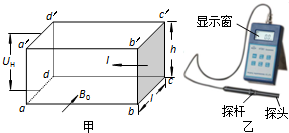

 (1)如图甲所示,某同学在做“研究匀变速直线运动”的实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T=0.10s,其中s1=5.12cm,s2=5.74cm,s3=6.14cm,s4=7.05cm,s5=7.68cm,s6=8.33cm、则打F点时小车的瞬时速度的大小是
(1)如图甲所示,某同学在做“研究匀变速直线运动”的实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T=0.10s,其中s1=5.12cm,s2=5.74cm,s3=6.14cm,s4=7.05cm,s5=7.68cm,s6=8.33cm、则打F点时小车的瞬时速度的大小是