题目内容
【题目】卫星A、B的运行方向相同,其中B为近地卫星,某时刻,两卫星相距最近(O、B、A在同一直线上),已知地球半径为R,卫星A离地心O的距离是卫星B离地心的距离的4倍,地球表面重力加速度为g,则( )
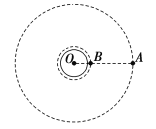
A.卫星A、B的运行周期的比值为![]()
B.卫星A、B的运行线速度大小的比值为![]()
C.卫星A、B的运行加速度的比值为![]()
D.卫星A、B至少经过时间t=![]() ,两者再次相距最近
,两者再次相距最近
【答案】BD
【解析】由地球对卫星的引力提供向心力G![]() =m
=m![]() r知T=2π
r知T=2π![]() ∝
∝![]() ,而rA=4rB,所以卫星A、B的运行周期的比值为
,而rA=4rB,所以卫星A、B的运行周期的比值为![]() =
=![]() ,A项错误;同理,由G
,A项错误;同理,由G![]() =m
=m ![]() 得v=
得v=![]() ∝
∝![]() ,所以卫星A、B的运行线速度大小的比值为
,所以卫星A、B的运行线速度大小的比值为![]() =
=![]() ,B项正确;
,B项正确;
由G![]() =ma得a=
=ma得a=![]() ∝
∝![]() ,所以卫星A、B的运行加速度的比值为
,所以卫星A、B的运行加速度的比值为![]() =
=![]() ,C项错误;由T=2π
,C项错误;由T=2π![]() 及地球表面引力等于重力大小G
及地球表面引力等于重力大小G![]() =mg知T=2π
=mg知T=2π![]() ,由于B为近地卫星,所以TB=2π
,由于B为近地卫星,所以TB=2π![]() ,当卫星A、B再次相距最近时,卫星B比卫星A多运行了一周,即 (
,当卫星A、B再次相距最近时,卫星B比卫星A多运行了一周,即 (![]() -
-![]() )t=2π,联立可得t=
)t=2π,联立可得t=![]() ,D项正确。
,D项正确。

练习册系列答案
相关题目