题目内容
（2013?崇明县一模）如图所示，abcd线圈中接有一灵敏电流计G，efgh线框的电阻不计，放在匀强磁场中．具有一定电阻的导体棒MN在恒力F作用下由静止开始向右运动，efgh线框足够长，则通过灵敏电流计G中的感应电流（ ）分析：本题有两次电磁感应，依次根据右手定则、楞次定律、法拉第电磁感应定律分析：
导体棒MN在恒力作用下做加速度逐渐减小的加速运动，根据右手定则判断MN中产生的感应电流谢，由楞次定律判断abcd中产生的感应电流方向．
根据法拉第电磁感应定律分析线框abcd中产生的感应电动势的变化，即可得知电流强度的变化．
导体棒MN在恒力作用下做加速度逐渐减小的加速运动，根据右手定则判断MN中产生的感应电流谢，由楞次定律判断abcd中产生的感应电流方向．
根据法拉第电磁感应定律分析线框abcd中产生的感应电动势的变化，即可得知电流强度的变化．
解答：解：导体棒MN向右运动时切割磁感线产生感应电流，由右手定则判断可知，MN中感应电流方向从M→N，由安培定则可知，穿过线框abcd的磁场方向向里．导体棒MN在恒力作用下做加速度逐渐减小的加速运动，感应电流增大，穿过线框abcd的磁通量增加，根据楞次定律判断得知，abcd中产生的感应电流方向为逆时针，则过灵敏电流计G中的感应电流方向为d到a．由于MN的加速度减小，产生的感应电流增加变慢，则穿过线框abcd的磁通量增加变慢，由法拉第电磁感应定律得知，abcd中产生的感应电动势减小，则知感应电流头减弱．
故选D
故选D
点评：本题是两次电磁感应的问题，是右手定则、安培定则、楞次定律和法拉第电磁感应定律的综合应用．
练习册系列答案
相关题目
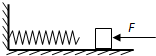（2013?崇明县一模）一物块在光滑的水平面上受一恒力F的作用而运动，在其正前方固定一个足够长的轻质弹簧，如图所示．当物块与弹簧接触后（ ）
（2013?崇明县一模）下图是一个遥控电动小车在水平直轨道上运动的v-t图象，图中2s～10s时间段的图象为曲线，其余时间段均为直线．已知小车运动过程中所受阻力不变，在2s～14s时间段内小车的功率保持不变，在14s末停止供电而让小车自由滑行，小车的质量为1.0kg．求：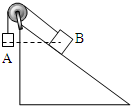
（2013?崇明县一模）如图所示，表面光滑的固定斜面顶端安装一个定滑轮，小物块A、B用轻绳连接并跨过滑轮（不计滑轮的质量和摩擦）．开始时A、B处于同一高度并恰好处于静止状态，现剪断轻绳后A自由下落，B沿斜面下滑．则在剪断轻绳到物块着地的过程中，两物块 （ ）