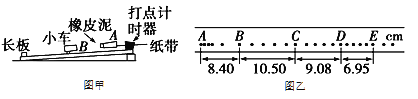
题目内容
【题目】如图所示,倾角α=30°的足够长光滑斜面固定在水平面上,斜面上放一长L=1.8 m、质量M =3 kg的薄木板,木板的最上端叠放一质量m=1 kg的小物块,物块与木板间的动摩擦因数μ=![]() .对木板施加沿斜面向上的恒力F,使木板沿斜面由静止开始做匀加速直线运动.设物块与木板间最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.
.对木板施加沿斜面向上的恒力F,使木板沿斜面由静止开始做匀加速直线运动.设物块与木板间最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.

(1)为使物块不滑离木板,求力F应满足的条件;
(2)若F=37.5 N,物块能否滑离木板?若不能,请说明理由;若能,求出物块滑离木板所用的时间及滑离木板后沿斜面上升的最大距离.
【答案】(1)F≤30N;(2)物块能滑离木板,1.2s,s=0.9m。
【解析】试题分析: (1)对M、m,由牛顿第二定律F-(M+m)gsinα=(M+m)a
对m,有f-mgsinα=ma
F≤mgcosα
代入数据得:F≤30N
(2)F=37.5N>30N,物块能滑离木板
对于M,有F-μmgcosα-Mgsinα=Ma1
对m,有μmgcosα-mgsinα=ma2
设物块滑离木板所用的时间为t,由运动学公式:![]() a1t2-
a1t2-![]() a2t2=L
a2t2=L
代入数据得:t=1.2s
物块离开木板时的速度v=a2t
由公式:-2gsinαs=0-v2
代入数据得s=0.9m

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目